题目内容
1.已知点A(0,2),抛物线C:y2=ax(a>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,MK垂直准线于点K,若|KM|:|MN|=1:$\sqrt{5}$,则a的值等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
分析 作出M在准线上的射影,根据|KM|:|MN|确定|KN|:|KM|的值,进而列方程求得a.
解答 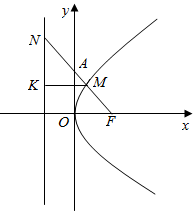 解:依题意F点的坐标为($\frac{a}{4}$,0),
解:依题意F点的坐标为($\frac{a}{4}$,0),
设M在准线上的射影为K,由抛物线的定义知|MF|=|MK|,
∴|KM|:|MN|=1:$\sqrt{5}$,
则|KN|:|KM|=2:1,
∵kFN=$\frac{0-2}{\frac{a}{4}-0}$=-$\frac{8}{a}$,kFN=-2,
∴$\frac{8}{a}=2$,解得a=4.
故选:D.
点评 本题主要考查了抛物线的简单性质.抛物线中涉及焦半径的问题常利用抛物线的定义转化为点到准线的距离来解决.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
18.在一球面上有A,B,C三点,如果AB=4$\sqrt{3}$,∠ACB=60°,球心O到平面ABC的距离为3,则球O的表面积为( )
| A. | 36π | B. | 64π | C. | 100π | D. | 144π |
13.“a3>b3”是“lna>lnb”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
10.点P(1,$\sqrt{2},\sqrt{3}$)为空间直角坐标系中的点,过点P作平面xOy的垂线PQ,垂足为Q,则点Q的坐标为( )
| A. | (0,$\sqrt{2}$,0) | B. | (0,$\sqrt{2},\sqrt{3}$) | C. | (1,0,$\sqrt{3}$) | D. | (1,$\sqrt{2}$,0) |
11.设a+b<0,且b>0,则下列不等式正确的是( )
| A. | b2>-ab | B. | a2<-ab | C. | a2<b2 | D. | a2>b2 |