题目内容
已知函数f(x)=-x2-x+ln(x+1)
(1)求函数y=f(x)的极值;
(2)若函数y=f(x)(x∈[0,2])的图象与直线y=-
x+m恰有两个公共点,求实数m的取值范围;
(3)证明:ln(n+1)<
+
+…+
(n∈N*).
(1)求函数y=f(x)的极值;
(2)若函数y=f(x)(x∈[0,2])的图象与直线y=-
| 5 |
| 2 |
(3)证明:ln(n+1)<
| 2 |
| 12 |
| 3 |
| 22 |
| n+1 |
| n2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值
专题:计算题,证明题,导数的综合应用,不等式的解法及应用
分析:(1)求出导数,由导数大于0,得增区间,导数小于0,得减区间,进而得到极值;
(2)函数y=f(x)(x∈[0,2])的图象与直线y=-
x+m恰有两个公共点,即为方程ln(x+1)+
x-x2=m在[0,2]有两个不相等的实数根.令g(x)=ln(x+1)+
x-x2,运用导数求出在区间[0,2]上的最值,即可得到m的范围;
(3)由(1)当x>-1时,f(x)在x=0处取得极大值0,也为最大值0,则ln(1+x)≤x+x2=x(1+x)
令x=
,得ln(1+
)=ln(1+n)-lnn<
,运用累加法,计算即可得证.
(2)函数y=f(x)(x∈[0,2])的图象与直线y=-
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(3)由(1)当x>-1时,f(x)在x=0处取得极大值0,也为最大值0,则ln(1+x)≤x+x2=x(1+x)
令x=
| 1 |
| n |
| 1 |
| n |
| 1+n |
| n2 |
解答:
(1)解:函数f(x)=-x2-x+ln(x+1)(x>-1)的导数为:
f′(x)=-2x-1+
=
,
当-1<x<0时,f′(x)>0,f(x)递增;当x>0时,f′(x)<0,f(x)递减.
则f(x)在x=0处取得极大值,且为0,无极小值.
(2)解:函数y=f(x)(x∈[0,2])的图象与直线y=-
x+m恰有两个公共点,
即为方程ln(x+1)+
x-x2=m在[0,2]有两个不相等的实数根.
令g(x)=ln(x+1)+
x-x2,g′(x)=
+
-2x=
,
当0<x<1时,g′(x)>0,g(x)递增;当1<x<2时,g′(x)<0,g(x)递减.
则g(x)在x=1时,取得最大值且为ln2+
,
由于g(0)=0,g(2)=ln3-1>0,
则有ln3-1≤m<ln2+
,
即有m的取值范围为[ln3-1,ln2+
);
(3)证明:由(1)当x>-1时,f(x)在x=0处取得极大值0,也为最大值0,
则ln(1+x)≤x+x2=x(1+x)
令x=
,得ln(1+
)=ln(1+n)-lnn<
,
∴ln2-ln1<
,ln3-ln2<
,…,
ln(1+n)-lnn<
,
上面n个不等式相加,得ln(1+n)-ln1<
+
+…+
(n∈N*),
则有ln(n+1)<
+
+…+
(n∈N*).
f′(x)=-2x-1+
| 1 |
| x+1 |
| -x(2x+3) |
| x+1 |
当-1<x<0时,f′(x)>0,f(x)递增;当x>0时,f′(x)<0,f(x)递减.
则f(x)在x=0处取得极大值,且为0,无极小值.
(2)解:函数y=f(x)(x∈[0,2])的图象与直线y=-
| 5 |
| 2 |
即为方程ln(x+1)+
| 3 |
| 2 |
令g(x)=ln(x+1)+
| 3 |
| 2 |
| 1 |
| x+1 |
| 3 |
| 2 |
| -4x2-x+5 |
| 2(x+1) |
当0<x<1时,g′(x)>0,g(x)递增;当1<x<2时,g′(x)<0,g(x)递减.
则g(x)在x=1时,取得最大值且为ln2+
| 1 |
| 2 |
由于g(0)=0,g(2)=ln3-1>0,
则有ln3-1≤m<ln2+
| 1 |
| 2 |
即有m的取值范围为[ln3-1,ln2+
| 1 |
| 2 |
(3)证明:由(1)当x>-1时,f(x)在x=0处取得极大值0,也为最大值0,
则ln(1+x)≤x+x2=x(1+x)
令x=
| 1 |
| n |
| 1 |
| n |
| 1+n |
| n2 |
∴ln2-ln1<
| 2 |
| 1 |
| 3 |
| 22 |
ln(1+n)-lnn<
| 1+n |
| n2 |
上面n个不等式相加,得ln(1+n)-ln1<
| 2 |
| 12 |
| 3 |
| 22 |
| n+1 |
| n2 |
则有ln(n+1)<
| 2 |
| 12 |
| 3 |
| 22 |
| n+1 |
| n2 |
点评:本题考查导数的运用:求单调区间和求极值、最值,考查函数和方程的转化思想,考查不等式的证明方法:运用函数的最值,由裂项相加,考查运算能力,属于中档题.

练习册系列答案
相关题目
曲线y=e
x在点(4,e2)处的切线与坐标轴所围三角形的面积为( )
| 1 |
| 2 |
| A、e2 | ||
| B、2e2 | ||
| C、4e2 | ||
D、
|
下列式子正确的是( )
A、(
| ||||||||||||
B、
| ||||||||||||
C、|
| ||||||||||||
D、
|
若向量
,
满足:|
|=
,|
|=2且(
-
)⊥
,则
与
的夹角是( )
| a |
| b |
| a |
| 2 |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
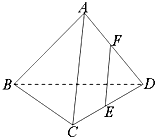 已知在空间四边形ABCD中,AC=AD,BC=BD,且E,F分别是CD,AD的中点.
已知在空间四边形ABCD中,AC=AD,BC=BD,且E,F分别是CD,AD的中点.