题目内容
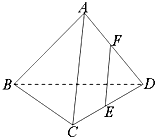 已知在空间四边形ABCD中,AC=AD,BC=BD,且E,F分别是CD,AD的中点.
已知在空间四边形ABCD中,AC=AD,BC=BD,且E,F分别是CD,AD的中点.(Ⅰ)求证:EF∥平面ABC;
(Ⅱ)求证:CD⊥AB.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)因为E,F分别是CD,AD的中点,利用中位线的性质得到EF∥AC,由线面平行的判定定理可证;
(Ⅱ)连结AE,BE,只要证明CD⊥平面ABE,再由线面垂直的性质可证.
(Ⅱ)连结AE,BE,只要证明CD⊥平面ABE,再由线面垂直的性质可证.
解答:
(Ⅰ)证明:因为E,F分别是CD,AD的中点,
所以,EF为△ACD的中位线,所以EF∥AC.…(2分)
又因为AC?平面ABC,EF?平面ABC,
所以,EF∥平面ABC.…(4分)
(Ⅱ)证明:连结AE,BE,
在△ACD中,因为AC=AD,E是CD中点,所以AE⊥CD.…(6分)
同理可证,BE⊥CD.…(7分)
又因为,AE∩BE=E,AE?平面ABE,BE?平面ABE,
所以,CD⊥平面ABE.…(9分)
又因为,AB?平面ABE,
所以CD⊥AB.…(10分)
所以,EF为△ACD的中位线,所以EF∥AC.…(2分)
又因为AC?平面ABC,EF?平面ABC,
所以,EF∥平面ABC.…(4分)
(Ⅱ)证明:连结AE,BE,
在△ACD中,因为AC=AD,E是CD中点,所以AE⊥CD.…(6分)
同理可证,BE⊥CD.…(7分)
又因为,AE∩BE=E,AE?平面ABE,BE?平面ABE,
所以,CD⊥平面ABE.…(9分)
又因为,AB?平面ABE,
所以CD⊥AB.…(10分)
点评:本题考查了线面平行的判定和线面垂直的性质定理和判定定理的运用,关键是熟练掌握相关的定理,正确运用.

练习册系列答案
相关题目
复数
的共轭复数是( )
| 5 |
| i-2 |
| A、-2+i | B、2+i |
| C、-2-i | D、2-i |
如图,△ABC内接于⊙O于A,AD切⊙O于A,∠BAD=60°,则∠ACB=( )


| A、120° | B、150° |
| C、90° | D、100° |