题目内容
已知,函数f(x)=2sin
在[-1,
]上具有单调性,求ω的范围为 .
| π•x |
| ω |
| 2 |
| 3 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:函数f(x)在[-1,
]上具有单调性,则当ω>0时,在该区间单调递增,当ω<0时单调递减,且函数f(x)=2sin
是奇函数,则函数f(x)=2sin
在[-1,1]上具有单调性,只需
≥2即可,从而可解得ω的范围.
| 2 |
| 3 |
| π•x |
| ω |
| π•x |
| ω |
| T |
| 2 |
解答:
解:函数f(x)=2sin
在[-1,
]上具有单调性,首先需明确:当ω>0时,在该区间单调递增,当ω<0时单调递减;其次,函数f(x)=2sin
是奇函数,故函数f(x)=2sin
在[-1,1]上具有单调性,只需
≥2即可,由T=
=2|ω|≥4,即可解得:|ω|≥2,故ω的范围为(-∞,-2]∪[2+∞).
故答案为:(-∞,-2]∪[2+∞).
| π•x |
| ω |
| 2 |
| 3 |
| π•x |
| ω |
| π•x |
| ω |
| T |
| 2 |
| 2π | ||
|
故答案为:(-∞,-2]∪[2+∞).
点评:本题主要考查了正弦函数的周期性,奇偶性,单调性,综合性较强,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
若f(x)=
,x1<x2<x3,且f (x1)=f (x2)=f (x3),则x1+x2+x3的值的范围是( )
|
| A、[1,2) |
| B、(1,2] |
| C、(0,1] |
| D、[2,3) |
设a=cos(2014π-
),函数f(x)=
则f(log2
)的值等于( )
| π |
| 3 |
|
| 1 |
| 6 |
A、
| ||
| B、4 | ||
C、
| ||
| D、6 |
复数
的共轭复数是( )
| 5 |
| i-2 |
| A、-2+i | B、2+i |
| C、-2-i | D、2-i |
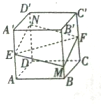 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,给出以下四个命题: