题目内容
曲线y=e
x在点(4,e2)处的切线与坐标轴所围三角形的面积为( )
| 1 |
| 2 |
| A、e2 | ||
| B、2e2 | ||
| C、4e2 | ||
D、
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,作图题,导数的综合应用
分析:由题意作图,求导y′=
e
x,从而写出切线方程为y-e2=
e2(x-4);从而求面积.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
 解:如图,y′=
解:如图,y′=
e
x;
故y′|x=4=
e2;
故切线方程为y-e2=
e2(x-4);
当x=0时,y=-e2,
当y=0时,x=2;
故切线与坐标轴所围三角形的面积S=
×2×e2=e2;
故选A.
 解:如图,y′=
解:如图,y′=| 1 |
| 2 |
| 1 |
| 2 |
故y′|x=4=
| 1 |
| 2 |
故切线方程为y-e2=
| 1 |
| 2 |
当x=0时,y=-e2,
当y=0时,x=2;
故切线与坐标轴所围三角形的面积S=
| 1 |
| 2 |
故选A.
点评:本题考查了导数的求法及曲线切线的求法,同时考查了数形结合的思想,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
双曲线
-
=1上一点P到左焦点F1的距离为9,则P到右焦点F2的距离是( )
| x2 |
| 16 |
| y2 |
| 20 |
| A、1 | B、17 |
| C、1或17 | D、23或41 |
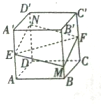 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,给出以下四个命题: