题目内容
已知抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线与该抛物线交于不同的两点A,B,且|AB|≤2p.
(1)求实数a的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,且p=4,求点N到直线l的距离.
(1)求实数a的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,且p=4,求点N到直线l的距离.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)设A、B的坐标和直线的方程,与抛物线方程联立消去y,由判别式大于0列出不等式,及x1+x2的和x1x2的表达式,由弦长公式求得AB的长度的表达式,根据|AB|的范围列出不等式,联立两个不等式求出a的范围;
(2)由(1)和条件得方程:x2-2(a+4)x+a2=0,由韦达定理得x1+x2的和x1x2的表达式,求出AB的中点坐标,再求出线段AB的垂直平分线方程,令y=0求出N的坐标,由点到直线的距离公式求出点N到直线l的距离.
(2)由(1)和条件得方程:x2-2(a+4)x+a2=0,由韦达定理得x1+x2的和x1x2的表达式,求出AB的中点坐标,再求出线段AB的垂直平分线方程,令y=0求出N的坐标,由点到直线的距离公式求出点N到直线l的距离.
解答:
解:(1)设直线l与抛物线两个不同的交点坐标为A(x1,y1)、B(x2,y2),
则过动点M(a,0)且斜率为1的直线l的方程为y=x-a,
将y=x-a代入y2=2px,得x2-2(a+p)x+a2=0,
所以△=4(a+p)2-4a2>0,即(a+p)2-a2>0,①
且x1+x2=2(a+p),x1x2=a2,
因为|AB|≤2p,
所以|AB|=
=
≤2p,②,
由①②得,-
<a≤-
,
所以实数a的取值范围是(-
,-
];
(2)由(1)得,将y=x-a代入y2=2px得,x2-2(a+p)x+a2=0,
又p=4,则上式为x2-2(a+4)x+a2=0,
则x1+x2=2(a+4),x1x2=a2,
所以AB的中点坐标D(a+4,4),
则线段AB的垂直平分线方程是:y-4=-(x-a-4),即y=-x+a+8,
令y=0代入得x=a+8,则N的坐标是(a+8,0),
所以点N到直线l的距离d=
=4
.
则过动点M(a,0)且斜率为1的直线l的方程为y=x-a,
将y=x-a代入y2=2px,得x2-2(a+p)x+a2=0,
所以△=4(a+p)2-4a2>0,即(a+p)2-a2>0,①
且x1+x2=2(a+p),x1x2=a2,
因为|AB|≤2p,
所以|AB|=
| (1+1)[(x1+x2)2-4x1x2] |
| 8p(2a+p) |
由①②得,-
| p |
| 2 |
| p |
| 4 |
所以实数a的取值范围是(-
| p |
| 2 |
| p |
| 4 |
(2)由(1)得,将y=x-a代入y2=2px得,x2-2(a+p)x+a2=0,
又p=4,则上式为x2-2(a+4)x+a2=0,
则x1+x2=2(a+4),x1x2=a2,
所以AB的中点坐标D(a+4,4),
则线段AB的垂直平分线方程是:y-4=-(x-a-4),即y=-x+a+8,
令y=0代入得x=a+8,则N的坐标是(a+8,0),
所以点N到直线l的距离d=
| |a+8-0-a| | ||
|
| 2 |
点评:本题考查直线与抛物线的位置关系,弦长公式、点到直线的距离公式,韦达定理等,考查运用解析几何的方法解决数学问题的能力.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
设a=cos(2014π-
),函数f(x)=
则f(log2
)的值等于( )
| π |
| 3 |
|
| 1 |
| 6 |
A、
| ||
| B、4 | ||
C、
| ||
| D、6 |
复数
的共轭复数是( )
| 5 |
| i-2 |
| A、-2+i | B、2+i |
| C、-2-i | D、2-i |
已知抛物线C:y2=2x上一点P到y轴的距离为3,则 P到焦点的距离为( )
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
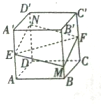 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,给出以下四个命题: