题目内容
若向量
，
满足：|
|=
，|
|=2且（
-
）⊥
，则
与
的夹角是（ ）
| a |
| b |
| a |
| 2 |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量垂直，数量积为0，得到（
-
）•
=0，展开得到夹角的余弦值的等式解之．
| a |
| b |
| a |
解答：
解：因为|
|=
，|
|=2且（
-
）⊥
，所以（
-
）•
=0，即
2-
•
=0，
所以2-
×2cos＜
，
＞=0，
解得cos＜
，
＞=
，
所以
与
的夹角是
；
故选B．
| a |
| 1 |
| 2 |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| a |
| b |
所以2-
| 2 |
| a |
| b |
解得cos＜
| a |
| b |
| ||
| 2 |
所以
| a |
| b |
| π |
| 4 |
故选B．
点评：本题考查了向量垂直的性质以及向量的数量积公式的运用求向量的夹角，属于基础题．
练习册系列答案
相关题目
双曲线
-
=1上一点P到左焦点F1的距离为9，则P到右焦点F2的距离是（ ）
| x2 |
| 16 |
| y2 |
| 20 |
| A、1 | B、17 |
| C、1或17 | D、23或41 |
对?x1，x2∈（0，
），若x2＞x1，且y1=
，y2=
，则（ ）
| π |
| 2 |
| 1+sinx1 |
| x1 |
| 1+sinx2 |
| x2 |
| A、y1=y2 |
| B、y1＞y2 |
| C、y1＜y2 |
| D、y1，y2的大小关系不能确定 |
方程
+
=1表示焦点在y轴的双曲线，则k的取值范围是（ ）
| x2 |
| k-3 |
| y2 |
| 2-k |
| A、k＜3 | B、k＜2 |
| C、2＜k＜3 | D、k＞2 |
函数f（x）=log2（2x）的图象大致是（ ）
A、 |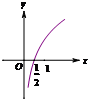
B、 |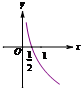
C、 |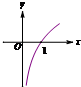
D、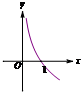 |