题目内容
已知函数f(x)是定义在R上的函数,满足f(x+y)=f(x)•f(y),且当x>0时,0<f(x)<1
(1)求证:f(0)=1;
(2)求证:当x∈R 时,恒有f(x)>0;
(3)求证:f(x)在 R 上是减函数;
(4)若f(2)=
,求不等式f(x)•f(3x2-1)<
的解.
(1)求证:f(0)=1;
(2)求证:当x∈R 时,恒有f(x)>0;
(3)求证:f(x)在 R 上是减函数;
(4)若f(2)=
| 1 |
| 9 |
| 1 |
| 27 |
考点:抽象函数及其应用
专题:证明题,函数的性质及应用
分析:(1)运用赋值法,令x=y=0,代入求出f(0),由条件舍去0,得到f(0)=1;
(2)由于f(0)=1,x>0时f(x)>0,只需x<0时,f(x)>0即可,令x+y=0,则f(x)f(-x)>0,对x讨论即可;
(3)运用函数的单调性定义证明,令x1<x2,则x2-x1>0,由x>0时,0<f(x)<1,得f(x2-x1)<1,再由f(x+y)=f(x)•f(y),得到f(x2-x1)=
,再由(2)得证;
(4)根据条件,令x=y=1,求出f(1),再令x=1,y=2,求出f(3)=
,再根据f(x+y)=f(x)•f(y)得到f(x+3x2-1)<f(3),再根据(2)得x+3x2-1>3,解出即可.
(2)由于f(0)=1,x>0时f(x)>0,只需x<0时,f(x)>0即可,令x+y=0,则f(x)f(-x)>0,对x讨论即可;
(3)运用函数的单调性定义证明,令x1<x2,则x2-x1>0,由x>0时,0<f(x)<1,得f(x2-x1)<1,再由f(x+y)=f(x)•f(y),得到f(x2-x1)=
| f(x2) |
| f(x1) |
(4)根据条件,令x=y=1,求出f(1),再令x=1,y=2,求出f(3)=
| 1 |
| 27 |
解答:
(1)证明:令x=y=0,则f(0)=f2(0),
即f(0)=0或f(0)=1,
令y=0,则f(x)=f(x)•f(0),
若f(0)=0,则f(x)=0,这与条件矛盾,
∴f(0)=1;
(2)证明:∵x=0时,f(0)=1,
x>0时,0<f(x)<1,
令x+y=0,则f(0)=f(x)•f(-x),
∵f(0)=1,∴f(x)•f(-x)=1>0,
若x>0,则-x<0,
∵f(x)>0,∴f(-x)>0,
∴当x∈R 时,恒有f(x)>0;
(3)证明:令x1<x2,则x2-x1>0,
∵x>0时,0<f(x)<1,
∴f(x2-x1)<1,
∵f(x+y)=f(x)•f(y),
∴f(x)=
,
∴f(x2-x1)=
<1,
由(2)得f(x2)<f(x1),
∴由函数单调性的定义得:
函数f(x)在 R 上是减函数;
(4)解:∵f(2)=
,f(x+y)=f(x)•f(y),
∴f(2)=f2(1),
∵f(x)>0,∴f(1)=
,
又f(3)=f(1)•f(2),
∴f(3)=
,
∴f(x)•f(3x2-1)<
即f(x)•f(3x2-1)<f(3),
∵f(x+y)=f(x)•f(y),∴f(x+3x2-1)<f(3),
∵函数f(x)在 R 上是减函数,
∴x+3x2-1>3即3x2+x-4>0,
∴x>1或x<-
,
∴原不等式的解集为:(1,+∞)∪(-∞,-
).
即f(0)=0或f(0)=1,
令y=0,则f(x)=f(x)•f(0),
若f(0)=0,则f(x)=0,这与条件矛盾,
∴f(0)=1;
(2)证明:∵x=0时,f(0)=1,
x>0时,0<f(x)<1,
令x+y=0,则f(0)=f(x)•f(-x),
∵f(0)=1,∴f(x)•f(-x)=1>0,
若x>0,则-x<0,
∵f(x)>0,∴f(-x)>0,
∴当x∈R 时,恒有f(x)>0;
(3)证明:令x1<x2,则x2-x1>0,
∵x>0时,0<f(x)<1,
∴f(x2-x1)<1,
∵f(x+y)=f(x)•f(y),
∴f(x)=
| f(x+y) |
| f(y) |
∴f(x2-x1)=
| f(x2) |
| f(x1) |
由(2)得f(x2)<f(x1),
∴由函数单调性的定义得:
函数f(x)在 R 上是减函数;
(4)解:∵f(2)=
| 1 |
| 9 |
∴f(2)=f2(1),
∵f(x)>0,∴f(1)=
| 1 |
| 3 |
又f(3)=f(1)•f(2),
∴f(3)=
| 1 |
| 27 |
∴f(x)•f(3x2-1)<
| 1 |
| 27 |
∵f(x+y)=f(x)•f(y),∴f(x+3x2-1)<f(3),
∵函数f(x)在 R 上是减函数,
∴x+3x2-1>3即3x2+x-4>0,
∴x>1或x<-
| 4 |
| 3 |
∴原不等式的解集为:(1,+∞)∪(-∞,-
| 4 |
| 3 |
点评:本题主要考查函数的单调性的判断及应用,注意运用定义证明,同时考查赋值法求函数值,这是解决抽象函数问题时常用的方法,一定要掌握.

练习册系列答案
相关题目
(文)从[0,3]中随机取一个数a,则事件“不等式|x+1|+|x-1|<a有解”发生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面中心得三棱锥)
已知正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面中心得三棱锥)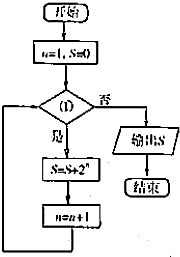 运行如图框图输出的S是254,则①应为
运行如图框图输出的S是254,则①应为