题目内容
已知定义在集合(0,+∞)的函数y=f(x)满足条件:对于任意的x,y∈(0,+∞),f(x•y)=f(x)+f(y),且当x>1时,f(x)>0 求证:
(1)对任意的x∈(0,+∞),有f(
)=-f(x);
(2)f(x)在(0,+∞)上是增函数.
(1)对任意的x∈(0,+∞),有f(
| 1 |
| x |
(2)f(x)在(0,+∞)上是增函数.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)利用赋值法求出f(1)的值,然后利用1=
•x,通过表达式求出结果即可.
(2)根据函数单调性的定义讨论函数的单调性.
| 1 |
| x |
(2)根据函数单调性的定义讨论函数的单调性.
解答:
解:(1)∵对于任意的x,y∈(0,+∞),f(x•y)=f(x)+f(y),
∴x=y=1时,f(1•1)=f(1)+f(1),
解得f(1)=0,
∵1=
•x,
∴f(
•x)=f(x)+f(
)=0,
∴f(
)=-f(x);
(2)设任意实数x1,x2∈(0,+∞),且x2<x1,
则f(x1)-f(x2)=f(
•x2)-f(x2)=f(
)+f(x2)-f(x2)=f(
).
∵x1,x2∈(0,+∞),x2<x1
∴
>1,又当x>1时有f(x)>0
∴f(
)>0即f(x1)-f(x2)>0
∴f(x1)>f(x2)函数在(0,+∞)是单调增函数.
∴x=y=1时,f(1•1)=f(1)+f(1),
解得f(1)=0,
∵1=
| 1 |
| x |
∴f(
| 1 |
| x |
| 1 |
| x |
∴f(
| 1 |
| x |
(2)设任意实数x1,x2∈(0,+∞),且x2<x1,
则f(x1)-f(x2)=f(
| x1 |
| x2 |
| x1 |
| x2 |
| x1 |
| x2 |
∵x1,x2∈(0,+∞),x2<x1
∴
| x1 |
| x2 |
∴f(
| x1 |
| x2 |
∴f(x1)>f(x2)函数在(0,+∞)是单调增函数.
点评:考查利用函数单调性的定义探讨抽象函数的单调性问题,对于解决抽象函数的一般采用赋值法,求某些点的函数值和证明不等式等,属中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
(理)(3x+5y-4z)7展开式的项数为( )
| A、21 | B、28 | C、36 | D、45 |

 在棱长为a的正方体A1B1C1D1-ABCD中,E,F分别为DD1,BB1的中点,G为线段D1F上一点.请判断直线AG与平面BEC1之间的位置关系,并给出证明.
在棱长为a的正方体A1B1C1D1-ABCD中,E,F分别为DD1,BB1的中点,G为线段D1F上一点.请判断直线AG与平面BEC1之间的位置关系,并给出证明.
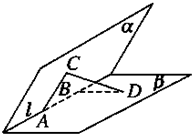 二面角α-l-β为60°,A、B是棱l上的两点,AC、BD分别在半平面α、β内,AC⊥l,BD⊥l,且AB=AC=a,BD=2a,则CD的长为
二面角α-l-β为60°,A、B是棱l上的两点,AC、BD分别在半平面α、β内,AC⊥l,BD⊥l,且AB=AC=a,BD=2a,则CD的长为