题目内容
3.下表是某厂改造后产量x吨产品与相应生产能耗y(吨)的几组对照数据:| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)已知技术改造前生产100吨该产品能耗90吨,试根据所求出的回归方程,预测生产100吨该产品的生产能耗比改造前降低多少吨?
附:$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
分析 (1)根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数$\widehat{b}$的公式,求得结果,再把样本中心点代入,求出$\widehat{a}$的值,得到线性回归方程.
(2)根据上一问所求的线性回归方程,把x=100代入线性回归方程,即可估计生产100吨甲产品的生产能耗.
解答 解:(1)$\overline{x}$=$\frac{1}{4}$(3+4+5+6)=4.5,
$\overline{y}$═$\frac{1}{4}$(2.5+3+4+4.4)=3.5,
故$\widehat{b}$=$\frac{\sum_{i=1}^{4}{{(x}_{i}y}_{i}-4\overline{x}•\overline{y})}{{{\sum_{i=1}^{4}x}_{i}}^{2}-{4\overline{x}}^{2}}$=0.7,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=0.35,
故$\widehat{y}$=0.7x+0.35…(8分)
(2)将x=100代入方程得:$\widehat{y}$=70.35,
生产100吨耗能70.35吨,降低90-70.35=19.65吨 …(12分)
点评 本题考查线性回归方程,两个变量之间的关系,除了函数关系,还存在相关关系,通过建立回归直线方程,就可以根据其部分观测值,获得对这两个变量之间整体关系的了解.

练习册系列答案
相关题目
13.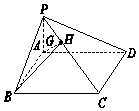 如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=$\frac{1}{2}$HC,点G在AH上,AG=mAH.四边形ABCD为平行四边形,若G,B,P,D四点共面,则实数m等于( )
如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=$\frac{1}{2}$HC,点G在AH上,AG=mAH.四边形ABCD为平行四边形,若G,B,P,D四点共面,则实数m等于( )
 如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=$\frac{1}{2}$HC,点G在AH上,AG=mAH.四边形ABCD为平行四边形,若G,B,P,D四点共面,则实数m等于( )
如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=$\frac{1}{2}$HC,点G在AH上,AG=mAH.四边形ABCD为平行四边形,若G,B,P,D四点共面,则实数m等于( )| A. | $\frac{1}{4}$ | B. | $\frac{4}{3}$P,D | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
15.若函数f(x)=$\left\{\begin{array}{l}{lo{g_{\frac{1}{2}}}x,0<x≤1}\\{-{x^2}+4x-3,x>1}\end{array}$,函数g(x)=f(x)-kx有两个零点,则k的值是( )
| A. | 0或$4-2\sqrt{3}$ | B. | $4+2\sqrt{3}$ | C. | 0 | D. | $4±2\sqrt{3}$ |
12.设复数z满足$\frac{1-i}{i}$•z=1,则|z|=( )
| A. | 1 | B. | 5 | C. | $\sqrt{2}$ | D. | 2 |
9.已知四棱锥P-ABCD,底面ABCD为矩形,点E,F在侧棱PA,PB上且PE=2EA,PF=2FB,点M为四棱锥内任一点,则M在平面EFCD上方的概率是( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{9}$ | C. | $\frac{7}{10}$ | D. | $\frac{5}{8}$ |