题目内容
18.(1)由数字1、2、3、4、5、6、7组成无重复数字的七位数,求三个偶数必相邻的七位数的个数及三个偶数互不相邻的七位数的个数;(2)六本不同的书,分为三组,求在下列条件下各有多少种不同的分配方法?
①每组两本;
②一组一本,一组二本,一组三本.
分析 根据题意,(1)若三个偶数必相邻,分3步进行分析:①、先将1、3、5、7四个奇数数字全排列,排好后,有5个空位可选,②、将3个偶数数字看成一个整体,③、在5个空位中任选1个,安排3个偶数数字这个整体,由分步计数原理计算可得答案,
若三个偶数互不相邻,分2步进行分析:①、先将1、3、5、7四个奇数数字全排列,有5个空位可选,②、在5个空位中,任选3个,安排三个偶数数字,由分步计数原理计算可得答案,
(2)①、由平均分组公司直接计算即可得答案;
②、分3步分析:先在6本书中先取出1本,作为一组,再在剩下的5本书中取出2本,作为一组,最后将余下的3本作为1组,由分步计数原理计算可得答案.
解答 解:(1)根据题意,若三个偶数必相邻,分3步进行分析:
①、先将1、3、5、7四个奇数数字全排列,有A44=24种情况,
排好后,有5个空位可选,
②、将3个偶数数字看成一个整体,考虑其顺序,有A33=6种情况,
③、在5个空位中任选1个,安排3个偶数数字这个整体,有5种情况,
则三个偶数必相邻的七位数有24×6×5=720个;
若三个偶数互不相邻,分2步进行分析:
①、先将1、3、5、7四个奇数数字全排列,有A44=24种情况,
排好后,有5个空位可选,
②、在5个空位中,任选3个,安排三个偶数数字,有A53=60种情况,
则三个偶数互不相邻的七位数有24×60=1440种;
(2)①根据题意,将6本书分成3组,每组2本,即将6本书平均分成3组,
有$\frac{C_6^2C_4^2C_2^2}{A_3^3}$=15种分组方法;
②将6本书分成3组,一组一本,一组二本,一组三本,
在6本书中先取出1本,作为一组,有C61种分发,
在剩下的5本书中取出2本,作为一组,有C52种分发,
将最后的3本作为1组,有C33种情况,
则共有$C_6^1C_5^2C_3^3$=60种分法.
点评 本题考查排列、组合的实际应用,(2)中注意平均分组与不平均分组公司的不同.

| A. | {x|x<3} | B. | {x|x≥5} | C. | {x|3≤x≤5} | D. | {x|3<x≤5} |
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{9}{8}$ | C. | $\frac{{3\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
| A. | 5 | B. | 8 | C. | 4 | D. | 2 |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)已知技术改造前生产100吨该产品能耗90吨,试根据所求出的回归方程,预测生产100吨该产品的生产能耗比改造前降低多少吨?
附:$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| A. | {3,4} | B. | {3,6} | C. | {1,3} | D. | {1,4} |
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | b<a<c |
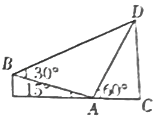 如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.
如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.