题目内容
甲、乙、丙三种食物的维生素A,B含量及成本如表:
某食物营养研究所想用x千克甲种食物,y千克乙种食物,z千克丙种食物配成100千克的混合食物,并使混合食物至少含56000单位维生素A和63000单位维生素B.
(1)用x,y表示混合物成本C;
(2)确定x,y,z的值,使成本最低.
| 甲 | 乙 | 丙 | |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素B(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
(1)用x,y表示混合物成本C;
(2)确定x,y,z的值,使成本最低.
考点:简单线性规划
专题:应用题,不等式的解法及应用
分析:(1)直接由题意得到x,y,z的关系,把z用含有x,y的代数式表示代入C=11x+9y+4z得答案;
(2)由题意列出关于x,y,z的不等式组,转化为关于x,y的不等式组,然后利用线性规划知识求得答案.
(2)由题意列出关于x,y,z的不等式组,转化为关于x,y的不等式组,然后利用线性规划知识求得答案.
解答:
 解:(1)由题意,x,y,z满足x+y+z=100,则z=100-x-y,
解:(1)由题意,x,y,z满足x+y+z=100,则z=100-x-y,
∴成本C=11x+9y+4z=7x+5y+400(元);
(2)依题意得不等式组
,
∵z=100-x-y,
∴
,
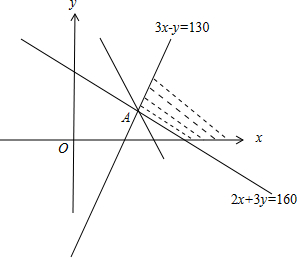
作出可行域如图,
联立
,解得A(50,20),
∴直线C=7x+5y+400过A时C最小为7×50+5×20+400=850.
∴x=50千克,y=30千克,z=20千克时成本最低.
 解:(1)由题意,x,y,z满足x+y+z=100,则z=100-x-y,
解:(1)由题意,x,y,z满足x+y+z=100,则z=100-x-y,∴成本C=11x+9y+4z=7x+5y+400(元);
(2)依题意得不等式组
|
∵z=100-x-y,
∴
|
作出可行域如图,
联立
|
∴直线C=7x+5y+400过A时C最小为7×50+5×20+400=850.
∴x=50千克,y=30千克,z=20千克时成本最低.
点评:本题考查了简单的线性规划,考查了简单的数学建模思想方法,关键是对题意的理解,是中档题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
一个几何体的三视图如图所示,该几何体的体积是( )


| A、16π | ||
| B、16 | ||
C、
| ||
D、
|
已知f(x)的图象如图所示,则下列数值按从小到大的排列顺序正确的是( )
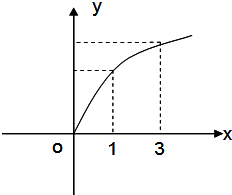

A、f′(1),f′(3),f(0),
| ||
B、f(0),f′(3),
| ||
C、
| ||
D、f(0),
|
下列函数f(x)中,满足“对定义域内的任意一个x都有f(-x)+f(x)=0,且在区间(0,+∞)上恒有
f′(x)>0”的是( )
f′(x)>0”的是( )
A、f(x)=
| ||
| B、f(x)=x2 | ||
| C、f(x)=x3 | ||
| D、f(x)=ex |