题目内容
设f（x）是定义在R上的奇函数，且当x＞0时，f（x）=2x-3，则f（-2）= ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：由奇函数性质得，f（-0）=-f（0），可得f（0）的值；再借助x＞0时，f（x）=2x-3，可将f（-2）转化为f（2）求解．
解答：
解：因为f（x）是定义在R上的奇函数，
又x＞0时，f（x）=2x-3，
所以f（-2）=-f（2）=-（22-3）=-1．
故答案为：-1．
又x＞0时，f（x）=2x-3，
所以f（-2）=-f（2）=-（22-3）=-1．
故答案为：-1．
点评：本题主要考查奇偶性的定义及其应用奇偶性求函数值，属基础题．
练习册系列答案
相关题目
已知△ABC中，AB=6，∠A=30°，∠B=120°，则△ABC的面积为（ ）
| A、9 | ||
| B、18 | ||
C、9
| ||
D、18
|
集合A={x|y=
}，B={y|y=x2-1}，则∁RA∪B=（ ）
| x2-4 |
| A、（-2，+∞） |
| B、[-2，+∞） |
| C、（-1，+∞） |
| D、[-1，+∞） |
某个几何体的三视图如图（其中正视图中的圆弧是半圆）所示，则该几何体的表面积为（ ）
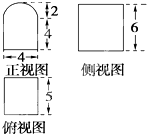
| A、92+24π |
| B、82+14π |
| C、92+14π |
| D、82+24π |
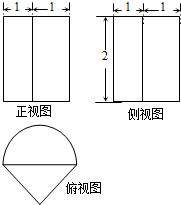如图是一个几何体的三视图，正视图和侧视图均为矩形，俯视图中曲线部分为半圆，尺寸如图，则该几何体的全面积为（ ）A、2+3π+4
| ||
B、2+2π+4
| ||
C、8+5π+2
| ||
D、6+3π+2
|
已知命题p：?x∈[1，2]，x2-a≥0，命题q：?x∈R使x2+2ax+2-a=0，若命题“p且q”为真，则实数a的取值范围是（ ）
| A、{a|-1＜a＜1或a＞1} |
| B、{a|a≥1} |
| C、{a|-2≤a≤1} |
| D、{a|a≤-2或a=1} |
若0＜b＜a＜1，则下列不等式成立的是（ ）
| A、ab＜b2＜1 | ||||||||
B、log
| ||||||||
| C、2b＜2a＜2 | ||||||||
| D、a2＜ab＜1 |