题目内容
已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(1-x),
(1)求函数的解析式,并画出函数图象;
(2)写出函数的单调区间及值域.
(1)求函数的解析式,并画出函数图象;
(2)写出函数的单调区间及值域.
考点:函数奇偶性的性质,函数的图象
专题:函数的性质及应用
分析:(1)因为x≥0时,f(x)=x(1-x),所以,当x<0时,-x>0,整体代入由函数的奇偶性可得答案;所得的函数解析式结合二次函数的图象特点,可函数的图象.
(2)根据图象写出单调区间和值域即可.
(2)根据图象写出单调区间和值域即可.
解答:
解:(1)因为x≥0时,f(x)=x(1-x),所以,当x<0时,-x>0,
∴f(-x)=-x(1+x),又因为f(x)为奇函数,所以f(-x)=-f(x),
∴-f(x)=-x(1+x),即f(x)=x(1+x)-------(4分)
综上f(x)=
-------------(6分)
由函数的解析式可得其图象,如图: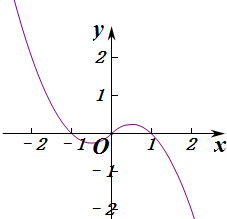
(2)由函数的图象可知:
增区间:[-
,
],
减区间:(-∞,-
),(
,+∞)
∴f(-x)=-x(1+x),又因为f(x)为奇函数,所以f(-x)=-f(x),
∴-f(x)=-x(1+x),即f(x)=x(1+x)-------(4分)
综上f(x)=
|
由函数的解析式可得其图象,如图:
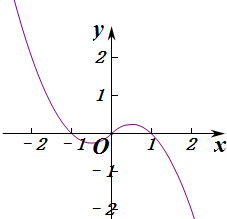
(2)由函数的图象可知:
增区间:[-
| 1 |
| 2 |
| 1 |
| 2 |
减区间:(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查函数在对称区间的解析式,以及函数图象的作法,属中档题.

练习册系列答案
相关题目
若函数f(x)=x3-3bx+b在(0,1)内有极小值,则( )
| A、b>0 | ||
| B、b<1 | ||
| C、0<b<1 | ||
D、b<
|
已知集合A={x|x-1|<2,x∈R},B={-1,0.1,2,3},则A∩B( )
| A、{0,1,2} |
| B、{-1,0,1,2} |
| C、{-1,0,2,3} |
| D、{0,1,2,3} |