题目内容
已知△ABC中，AB=6，∠A=30°，∠B=120°，则△ABC的面积为（ ）
| A、9 | ||
| B、18 | ||
C、9
| ||
D、18
|
考点：三角形的面积公式
专题：计算题
分析：先画出草图，由RT△的边角关系，求出底和高，从而求出三角形的面积．
解答：
解：如图示：
，
由∠A=30°，∠B=120°得∠c=30°，
∴△ABC是等腰三角形，AB=BC，
作BD⊥AC垂足为D，
在RT△ABD中，
由AB=6，∠A=30°，得出：BD=3，AD=3
，
∴AC=6
，
∴S△ABC=
×6
×3=9
；
故选：D．
，由∠A=30°，∠B=120°得∠c=30°，
∴△ABC是等腰三角形，AB=BC，
作BD⊥AC垂足为D，
在RT△ABD中，
由AB=6，∠A=30°，得出：BD=3，AD=3
| 3 |
∴AC=6
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
故选：D．
点评：本题考查了直角三角形的边角关系，考查三角形的面积公式，是一道基础题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
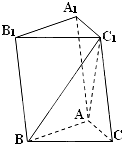如图，斜三棱柱ABC-A1B1C1中，AB=3，AC=2，AB⊥AC，A1C1⊥BC1侧棱与底面成60°角．