Question

三棱柱P-ABC中，PA，PB，PC两两垂直，设∠APO=α，∠BPO=β，∠CPO=γ．O为△ABC一点，求tanαtanβtanγ的取值范围．

Answer 1

考点：棱柱的结构特征

专题：空间位置关系与距离

分析：以P作为长方体的顶点，以O作为长方体体对角线的另一个顶点，建立长方体，如图，将∠APO=α，∠BPO=β，∠CPO=γ转为∠EPO=∠APO，∠BPO=∠MPO，∠CPO=∠GPO，借助于长方体的性质解答．

解答： 解：因为PA，PB，PC两两垂直，设∠APO=α，∠BPO=β，∠CPO=γ．O为△ABC一点，以O为长方体的一个顶点，在PA，PB，PC上设PE=a，PM=b，PG=c，如图，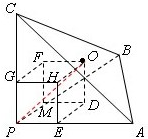
则∠EPO=∠APO，∠BPO=∠MPO，∠CPO=∠GPO，
所以tanα=

c2+b2

a

≥

2bc

a

，当且仅当b=c时取等号，
tanβ=

a2+c2

b

≥

2ac

b

，当且仅当a=c时取等号；
tanγ=

a2+b2

c

≥

2ab

c

，当且仅当a=b时取等号；
所以tanαtanβtanγ≥2

2

．

点评：本题考查了构造长方体解决空间角的问题，方法灵活．