题目内容
以下四个命题中,正确的是( )
A、△ABC为直角三角形的充要条件是
| ||||||||||||||||||
B、若
| ||||||||||||||||||
C、若{
| ||||||||||||||||||
D、|(
|
考点:命题的真假判断与应用
专题:平面向量及应用,空间向量及应用
分析:A.由
•
=0,利用数量积定义可得∠BAC=90°,即△ABC为直角三角形,反之不成立;
B.由
=
+
,可知
+
≠1,利用向量共线定理即可判断出;
C.利用基底的意义即可判断出;
D.左边=|
| |
| |cos<
,
>| |
|,右边=|
| |
| |
|,即可判断出.
| AB |
| AC |
B.由
| OP |
| 1 |
| 2 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 2 |
| 1 |
| 3 |
C.利用基底的意义即可判断出;
D.左边=|
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
解答:
解:A.由
•
=0⇒|
| |
|cos∠BAC=0⇒cos∠BAC=0⇒∠BAC=90°,即△ABC为直角三角形.
反之不成立,因此
•
=0是△ABC为直角三角形的充分不必要条件,因此不正确;
B.∵
=
+
,可知
+
≠1,因此P、A、B三点不共线,因此不正确;
C.假设存在实数满足
+
=λ(
+
)+μ(
+
),化为(λ-1)
+(λ+μ)
+(μ-1)
=
,
∵{
,
,
}为空间的一个基底,∴
,此方程组无解,因此假设不成立.
∴{
+
,
+
,
+
}也构成空间的一个基底,因此正确.
D.左边=|
| |
| |cos<
,
>| |
|,右边=|
| |
| |
|,
因此左边=右边不恒成立,故不正确.
综上可知:只有D正确.
故选:D.
| AB |
| AC |
| AB |
| AC |
反之不成立,因此
| AB |
| AC |
B.∵
| OP |
| 1 |
| 2 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 2 |
| 1 |
| 3 |
C.假设存在实数满足
| c |
| a |
| a |
| b |
| b |
| c |
| a |
| b |
| c |
| 0 |
∵{
| a |
| b |
| c |
|
∴{
| a |
| b |
| b |
| c |
| c |
| a |
D.左边=|
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
因此左边=右边不恒成立,故不正确.
综上可知:只有D正确.
故选:D.
点评:本题综合考查了数量积的意义、空间向量的基底、向量共线定理等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
已知双曲线
-
=1的一条渐近线方程为y=
x,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
设A是半径为1的圆周上一定点,P是圆周上一动点,则弦PA<1的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
取一根长度为4米的绳子,拉直后在任意位置剪断,那么剪得的两段都不少于1米的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知菱形ABCD的边长为4,∠ABC=150°,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率( )
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
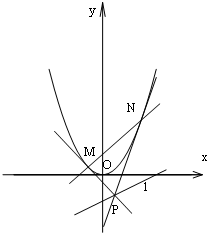 已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示.
已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示.