题目内容

取一根长度为4米的绳子，拉直后在任意位置剪断，那么剪得的两段都不少于1米的概率是（　　）
A、
1
4
B、
1
3
C、
1
2
D、
2
3
考点：几何概型
专题：概率与统计
分析：因为绳子的总长为4m，所以只能在绳子中间2m的部分剪断，才能使剪出的两段符合条件．由此结合几何概型的概率公式，不难得到本题答案．
解答： 解：记“两段绳子的长都不小于1m”为事件A，
∵绳子的总长为4米，而剪得两段绳子的长都不小于1m
∴如图所示，只能在中间2m的部分剪断，才能使剪出的两段符合条件

根据几何概型的概率公式，可得事件A发生的概率 P（A）=
1
2
．
故选：C．
点评：本题给出4米长的绳子，求使剪出的两段绳子的长都不小于1m的概率．着重考查了几何概型及其计算公式等知识，属于基础题．
练习册系列答案
相关题目
若某程序框图如图所示，则该程序运行后输出的i值为
 
在平面直角坐标系中，定点M（1，0），两动点A，B在双曲线x2-3y2=3的右支上，则cos∠AMB的最小值是（　　）
A、-
1
2
B、
1
2
C、-
1
3
D、
1
3
从集合{2，3，4，5}中随机抽取一个数a，从集合{1，3，5}中随机抽取一个数b，则向量
m
=(a，b)与向量
n
=(1，-1)垂直的概率为（　　）
A、
1
6
B、
1
3
C、
1
4
D、
1
2
以下四个命题中，正确的是（　　）
A、△ABC为直角三角形的充要条件是
AB
•
AC
=0
B、若
OP
=
1
2
OA
+
1
3
OB
，则P、A、B三点共线
C、若{
a
，
b
，
c
}为空间的一个基底，则{
a
+
b
，
b
+
c
，
c
+
a
}也构成空间的一个基底
D、|(
a
•
b
)•
c
|=|
a
|•|
b
|•|
c
|
设集合M={x|x2≥4}，N={x|x+1≥0}，则（∁RM）∩N=（　　）
A、{x|-1≤x＜2}
B、{x|x＜2}
C、{x|-1＜x＜2}
D、{x|x≤2}
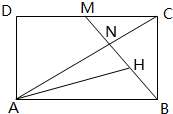如图，M是矩形ABCD的边CD上的一点，AC与BM相交于点N，BN=
2
3
BM．
（1）求证：M是CD的中点；
（2）若AB=2，BC=1，H是BM上异于B的一动点，求
AH
•
HB
的最小值．
在周长为定值的△DEC中，已知|DE|=8，动点C的运动轨迹为曲线G，且当动点C运动时，cosC有最小值-
7
25
．
（1）以DE所在直线为x轴，线段DE的中垂线为y轴建立直角坐标系，求曲线G的方程；
（2）直线l分别切椭圆G与圆M：x2+y2=R2（其中3＜R＜5）于A、B两点，求|AB|的范围．
已知双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)，直线l：y=
3
(x-4)关于直线l1：y=
b
a
x对称的直线l′与x轴平行．
（1）求双曲线的离心率；
（2）若点M（4，0）到双曲线上的点P的最小距离等于1，求双曲线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网