题目内容
下列说法:其中正确的个数是 .
①命题“?x∈R,2x≤0”的否定是“?x∈R,2x>0”;
②关于x的不等式a<sin2x+
恒成立,则a的取值范围是a<3;
③对于函数f(x)=
(a∈R且a≠0),则有当a=1时,?k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点.
①命题“?x∈R,2x≤0”的否定是“?x∈R,2x>0”;
②关于x的不等式a<sin2x+
| 2 |
| sin2x |
③对于函数f(x)=
| ax |
| 1+|x| |
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①利用命题的否定即可判断出;
②令sin2x=t∈(0,1],f(t)=t+
.求出f(t)的最小值即可;
③对于函数f(x)=
(a∈R且a≠0),当a=1时,假设k∈(1,+∞),则g(x)=
-kx为R上的奇函数.利用奇函数的性质和导数研究g(x)在x>0时的单调性即可.
②令sin2x=t∈(0,1],f(t)=t+
| 2 |
| t |
③对于函数f(x)=
| ax |
| 1+|x| |
| x |
| 1+|x| |
解答:
解:①命题“?x∈R,2x≤0”的否定是“?x∈R,2x>0”,正确;
②令sin2x=t∈(0,1],f(t)=t+
.
则关于x的不等式a<sin2x+
恒成立?a<f(t)min.
由f′(t)=1-
=
<0,可知函数f(t)在(0,1]上单调递减,
∴f(t)min=f(1)=3.
∴a的取值范围是a<3.
因此正确.
③对于函数f(x)=
(a∈R且a≠0),当a=1时,假设k∈(1,+∞),
则g(x)=
-kx为R上的奇函数.
当x=0时,g(0)=0,可知0是函数g(x)的一个零点.
当x>0时,g(x)=
-kx,则g′(x)=
-k<0,
∴函数g(x)在0,+∞)上单调递减,又函数g(x)在x=0处连续,∴g(x)<g(0)=0.
∴当x>0时,函数g(x)不存在零点.
由奇函数的性质可知:当x<0时,函数g(x)也不存在零点.
综上可知:函数g(x)有且仅有一个零点.
因此③不正确.
综上可知:只有①②正确.
故答案为:2.
②令sin2x=t∈(0,1],f(t)=t+
| 2 |
| t |
则关于x的不等式a<sin2x+
| 2 |
| sin2x |
由f′(t)=1-
| 2 |
| t2 |
| t2-2 |
| t2 |
∴f(t)min=f(1)=3.
∴a的取值范围是a<3.
因此正确.
③对于函数f(x)=
| ax |
| 1+|x| |
则g(x)=
| x |
| 1+|x| |
当x=0时,g(0)=0,可知0是函数g(x)的一个零点.
当x>0时,g(x)=
| x |
| 1+x |
| 1 |
| (1+x)2 |
∴函数g(x)在0,+∞)上单调递减,又函数g(x)在x=0处连续,∴g(x)<g(0)=0.
∴当x>0时,函数g(x)不存在零点.
由奇函数的性质可知:当x<0时,函数g(x)也不存在零点.
综上可知:函数g(x)有且仅有一个零点.
因此③不正确.
综上可知:只有①②正确.
故答案为:2.
点评:本题考查了利用导数研究函数的单调性、函数的零点、最小值等基础知识与基本技能方法,考查了分析问题和解决问题的能力,属于难题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
在平面直角坐标系中,定点M(1,0),两动点A,B在双曲线x2-3y2=3的右支上,则cos∠AMB的最小值是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
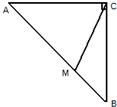
如图,在等腰直角三角形ABC中,在斜边AB上找一点M,则AM<AC的概率为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
以下四个命题中,正确的是( )
A、△ABC为直角三角形的充要条件是
| ||||||||||||||||||
B、若
| ||||||||||||||||||
C、若{
| ||||||||||||||||||
D、|(
|