题目内容
已知双曲线
-
=1的一条渐近线方程为y=
x,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据双曲线
-
=1的一条渐近线方程为y=
x,可得
=
,从而可求双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
解答:
解:∵双曲线
-
=1的一条渐近线方程为y=
x,
∴
=
,
∴e=
=
=
.
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
∴
| b |
| a |
| 1 |
| 2 |
∴e=
| c |
| a |
1+(
|
| ||
| 2 |
故选:A.
点评:本题考查双曲线的离心率的求法,解题时要认真审题,要熟练掌握双曲线的离心率、渐近线方程等基础知识.

练习册系列答案
相关题目
在平面直角坐标系中,定点M(1,0),两动点A,B在双曲线x2-3y2=3的右支上,则cos∠AMB的最小值是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
如图,在等腰直角三角形ABC中,在斜边AB上找一点M,则AM<AC的概率为( )
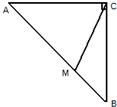

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
以下四个命题中,正确的是( )
A、△ABC为直角三角形的充要条件是
| ||||||||||||||||||
B、若
| ||||||||||||||||||
C、若{
| ||||||||||||||||||
D、|(
|
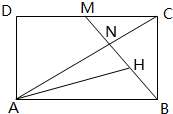 如图,M是矩形ABCD的边CD上的一点,AC与BM相交于点N,BN=
如图,M是矩形ABCD的边CD上的一点,AC与BM相交于点N,BN=