题目内容
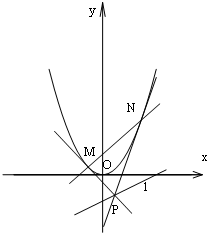已知抛物线C：y=x2，直线l：x-2y-2=0，点P是直线l上任意一点，过点P作抛物线C的切线PM，PN，切点分别为M，N，直线PM，PN斜率分别为k1，k2，如图所示．（1）若P（4，1），求证：k1+k2=16；
（2）当P在直线l上运动时，求证：直线MN过定点，并求出该定点坐标．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）设过P的切线方程为：y-1=k（x-4），代入抛物线C得：x2-kx+4k-1=0，由△=0，能证明k1+k2=16．
（2）设P（x0，y0），x0-2y0=2，切点M（x1，y1），N（x2，y2）对y=x2求导数，推导出直线PM：y-y1=2x1（x-x1），直线PN：y-y2=2x2（x-x2），由此能证明MN过定点(
， 1)．
（2）设P（x0，y0），x0-2y0=2，切点M（x1，y1），N（x2，y2）对y=x2求导数，推导出直线PM：y-y1=2x1（x-x1），直线PN：y-y2=2x2（x-x2），由此能证明MN过定点(
| 1 |
| 4 |
解答：
（1）证明：设过P的切线方程为：y-1=k（x-4），
代入抛物线C，消去y得：x2-kx+4k-1=0，
由△=k2-4（4k-1）=0，
∴k2-16k+4=0，
∵该方程的两个根为直线PM，PN斜率k1，k2，
∴k1+k2=16．（5分）
（2）证明：设P（x0，y0），x0-2y0=2，切点M（x1，y1），N（x2，y2）
对y=x2求导数，y'=2x，
∴k1=2x1，k2=2x2
∴直线PM：y-y1=2x1（x-x1），直线PN：y-y2=2x2（x-x2），
∵y1=
，y2=
，
∴直线PM：y=2x1x-y1，直线PN：y=2x2x-y2，
∵直线PM，PN都过点P，∴2x0x1-y1=y0，2x0x2-y2=y0，
这说明M（x1，y1），N（x2，y2）满足直线2x0x-y=y0的方程，
∴直线MN为：2x0x-y=y0，∵x0-2y0=2，
∴MN为：4x0(x-
)=2(y-1)，x0∈R，即MN过定点(
， 1)．（12分）
代入抛物线C，消去y得：x2-kx+4k-1=0，
由△=k2-4（4k-1）=0，
∴k2-16k+4=0，
∵该方程的两个根为直线PM，PN斜率k1，k2，
∴k1+k2=16．（5分）
（2）证明：设P（x0，y0），x0-2y0=2，切点M（x1，y1），N（x2，y2）
对y=x2求导数，y'=2x，
∴k1=2x1，k2=2x2
∴直线PM：y-y1=2x1（x-x1），直线PN：y-y2=2x2（x-x2），
∵y1=
| x | 2 1 |
| x | 2 2 |
∴直线PM：y=2x1x-y1，直线PN：y=2x2x-y2，
∵直线PM，PN都过点P，∴2x0x1-y1=y0，2x0x2-y2=y0，
这说明M（x1，y1），N（x2，y2）满足直线2x0x-y=y0的方程，
∴直线MN为：2x0x-y=y0，∵x0-2y0=2，
∴MN为：4x0(x-
| 1 |
| 4 |
| 1 |
| 4 |
点评：本题考查两直线的斜率之和为16的证明，考查直线过定点的证明，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
相关题目
以下四个命题中，正确的是（ ）
A、△ABC为直角三角形的充要条件是
| ||||||||||||||||||
B、若
| ||||||||||||||||||
C、若{
| ||||||||||||||||||
D、|(
|