题目内容
设A是半径为1的圆周上一定点，P是圆周上一动点，则弦PA＜1的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：概率与统计
分析：根据已知中A是圆上固定的一定点，在圆上其他位置任取一点P，连接A、P两点，它是一条弦，我们求出B点位置所有基本事件对应的弧长，及满足条件PA长小于1的基本事件对应的弧长，代入几何概型概率计算公式，即可得到答案．
解答：
解：在圆上其他位置任取一点P，圆半径为1，
则P点位置所有情况对应的弧长为圆的周长2π，
其中满足条件PA＜1的对应的弧长为
•2π•1，
则AB弦的长度大于等于半径长度的概率P=
=
，
故选：A．
解：在圆上其他位置任取一点P，圆半径为1，则P点位置所有情况对应的弧长为圆的周长2π，
其中满足条件PA＜1的对应的弧长为
| 1 |
| 3 |
则AB弦的长度大于等于半径长度的概率P=
| ||
| 2π |
| 1 |
| 3 |
故选：A．
点评：本题考查的知识点是几何概型，其中根据已知条件计算出所有基本事件对应的几何量及满足条件的基本事件对应的几何量是解答的关键．
练习册系列答案
新思维寒假作业系列答案
相关题目
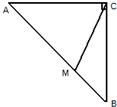
如图，在等腰直角三角形ABC中，在斜边AB上找一点M，则AM＜AC的概率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知全集U={-2，-1，0，1，2，3，4，5，6}，集合M={大于-1且小于4的整数}，则∁UM=（ ）
| A、∅ |
| B、{-2，-1，5，6} |
| C、{0，1，2，3，4} |
| D、{-2，-1，4，5，6} |
以下四个命题中，正确的是（ ）
A、△ABC为直角三角形的充要条件是
| ||||||||||||||||||
B、若
| ||||||||||||||||||
C、若{
| ||||||||||||||||||
D、|(
|
在区间[-2，3]上任取一个数a，则函数f（x）=x2-2ax+a+2有零点的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|