题目内容
已知A、B是椭圆
+
=1的左、右顶点,椭圆上异于A、B的两点C、D和x轴上一点P,满足
=
+
.
(1)设△ADP、△ACP、△BCP、△BDP的面积分别为S1、S2、S3、S4,求证:S1S3=S2S4;
(2)设P点的横坐标为x0,求x0的取值范围.
| x2 |
| 4 |
| y2 |
| 3 |
| AP |
| 1 |
| 3 |
| AD |
| 2 |
| 3 |
| AC |
(1)设△ADP、△ACP、△BCP、△BDP的面积分别为S1、S2、S3、S4,求证:S1S3=S2S4;
(2)设P点的横坐标为x0,求x0的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
=
,C、D、P三点共线,且C、D在P点的两侧,由此能够证明S1S3=S2S4.
(2)设直线CD的方程为:x=my+x0由
,得:(3m2+4)y2+6mx0y+3x02-12=0,由此利用韦达定理结合已知条件能求出x0的取值范围.
| CP |
| 1 |
| 3 |
| CD |
(2)设直线CD的方程为:x=my+x0由
|
解答:
(1)证明:∵
=
+
,∴
=
+(1-
)
,
即
-
=
(
-
),
∴
=
,
∴C、D、P三点共线,且C、D在P点的两侧,
∵△ADP、△ACP、△BCP、△BDP的面积分别为S1、S2、S3、S4,
∴
=
=
,∴S1S3=S2S4.
(2)解:由(Ⅰ)知,C、D、P三点共线,且C、D在P点的两侧,且C、D异于A、B的两点,
∴-2<x0<2,且直线CD不平行于x轴,
设直线CD的方程为:x=my+x0
由
,得:(3m2+4)y2+6mx0y+3x02-12=0,
当-2<x0<2时,直线与椭圆有两个交点,
设C(x1,y1),D(x2,y2),
∴y1+y2=-
,y1y2=
,
又
=
,∴y2=-2y1,
联立三式,消去y1、y2 得:-
=
,
化简得:(27x02-12)m2=4(4-x02),
∵-2<x0<2,m2>0,∴27x02-12>0,
所以x0>
或x0<-
,
综上知x0的取值范围是(-2,-
)∪(
,2).
| AP |
| 1 |
| 3 |
| AD |
| 2 |
| 3 |
| AC |
| AP |
| 1 |
| 3 |
| AD |
| 1 |
| 3 |
| AC |
即
| AP |
| AC |
| 1 |
| 3 |
| AD |
| AC |
∴
| CP |
| 1 |
| 3 |
| CD |
∴C、D、P三点共线,且C、D在P点的两侧,
∵△ADP、△ACP、△BCP、△BDP的面积分别为S1、S2、S3、S4,
∴
| S1 |
| S2 |
|
| ||
|
|
| S4 |
| S3 |
(2)解:由(Ⅰ)知,C、D、P三点共线,且C、D在P点的两侧,且C、D异于A、B的两点,
∴-2<x0<2,且直线CD不平行于x轴,
设直线CD的方程为:x=my+x0
由
|
当-2<x0<2时,直线与椭圆有两个交点,
设C(x1,y1),D(x2,y2),
∴y1+y2=-
| 6mx0 |
| 3m2+4 |
| 3x02-12 |
| 3m2+4 |
又
| CP |
| 1 |
| 3 |
| CD |
联立三式,消去y1、y2 得:-
| 72m2x02 |
| (3m2+4)2 |
| 3x02-12 |
| 3m2+4 |
化简得:(27x02-12)m2=4(4-x02),
∵-2<x0<2,m2>0,∴27x02-12>0,
所以x0>
| 2 |
| 3 |
| 2 |
| 3 |
综上知x0的取值范围是(-2,-
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查三角形面积乘积相等的证明,考查实数的取值范围的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
以下四个命题中,正确的是( )
A、△ABC为直角三角形的充要条件是
| ||||||||||||||||||
B、若
| ||||||||||||||||||
C、若{
| ||||||||||||||||||
D、|(
|
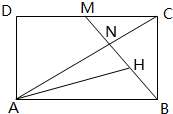 如图,M是矩形ABCD的边CD上的一点,AC与BM相交于点N,BN=
如图,M是矩形ABCD的边CD上的一点,AC与BM相交于点N,BN=