题目内容
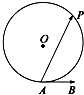如图，A是半径为5的圆O上的一个定点，单位向量| AB |
| AP |
| AB |
| A、（-5，5） | ||||
| B、[-5，5] | ||||
C、(-
| ||||
| D、[0，5] |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图所示：设∠PAB=θ，作OM⊥AP，则∠AOM=θ，求得AP=2AM=10sinθ，可得
•
=10sinθ×1×cosθ=5sin2θ，由此求得
•
的取值范围．
| AP |
| AB |
| AP |
| AB |
解答：
解：如图所示：设∠PAB=θ，作OM⊥AP，则∠AOM=θ，
∴sinθ=
，AM=5sinθ，AP=2AM=10sinθ．
∴
•
=10sinθ×1×cosθ=5sin2θ∈[-5，5]．
故选B．
解：如图所示：设∠PAB=θ，作OM⊥AP，则∠AOM=θ，∴sinθ=
| AM |
| OA |
∴
| AP |
| AB |
故选B．
点评：本题主要考查了向量的数量积的定义，弦切角定理及三角函数的定义的综合应用，试题具有一定的灵活性，属于中档题．
练习册系列答案
相关题目
将号码分别为1，2，3，4的四张完全相同的纸片放入一口袋中，甲从袋中摸出一个纸片，其号码为a，放回后，乙从此口袋中再摸出一纸片，其号码为b，则使不等式a-2b+1＜0成立的事件发生的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
点M是曲线
+
=1（x≠±5）上任意一点，点A，B的坐标分别为（-5，0），（5，0），直线AM与直线BM的斜率之积为（ ）
| x2 |
| 25 |
| y2 |
| 9 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
不等式
≥0的解集是（ ）
| (x-2)(10-x) |
| (x-1) |
| A、{x|2≤x≤10或x＜1} |
| B、{x|2≤x≤10或x≤1} |
| C、{x|1＜x≤2或x≥10} |
| D、{x|1≤x≤2或x≥10} |