题目内容
点M是曲线
+
=1（x≠±5）上任意一点，点A，B的坐标分别为（-5，0），（5，0），直线AM与直线BM的斜率之积为（ ）
| x2 |
| 25 |
| y2 |
| 9 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
考点：椭圆的简单性质
专题：平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析：利用椭圆的参数方程，可设M（5sinx，3cosx），结合点A，B的坐标分别为（-5，0），（5，0），即可求得kAM•kBM的值．
解答：
解：∵点M是曲线
+
=1（x≠±5）上任意一点，
∴设M坐标为（5sinx，3cosx），
又∵点A，B的坐标分别为（-5，0），（5，0），
∴kAM=
，kBM=
kAM•kBM=
•
=
=-
=-
，
故选：A
| x2 |
| 25 |
| y2 |
| 9 |
∴设M坐标为（5sinx，3cosx），
又∵点A，B的坐标分别为（-5，0），（5，0），
∴kAM=
| 3cosx |
| 5sinx+5 |
| 3cosx |
| 5sinx-5 |
kAM•kBM=
| 3cosx |
| 5sinx+5 |
| 3cosx |
| 5sinx-5 |
| 9cos2x |
| 25sin2x-25 |
| 9cos2x |
| 25cos2x |
| 9 |
| 25 |
故选：A
点评：本题主要考查直线与椭圆的位置关系，合理利用椭圆的参数方程设点的坐标，可以简化计算，属于中档题．
练习册系列答案
相关题目
如图所示，点M在正六边形ABCDEF的边BC、CD、DE、EF上变动，若如直线l1、l2的斜率是二次方程x2-4x+1=0的两根，那么l1与l2的夹角是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
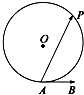如图，A是半径为5的圆O上的一个定点，单位向量| AB |
| AP |
| AB |
| A、（-5，5） | ||||
| B、[-5，5] | ||||
C、(-
| ||||
| D、[0，5] |