题目内容
将号码分别为1,2,3,4的四张完全相同的纸片放入一口袋中,甲从袋中摸出一个纸片,其号码为a,放回后,乙从此口袋中再摸出一纸片,其号码为b,则使不等式a-2b+1<0成立的事件发生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:每次摸出的号码(a,b)共有 4×4=16 个,满足a-2b+1<0的共有10个,由此使不等式a-2b+1<0成立的事件发生的概率
解答:
解:每次摸出的号码(a,b)共有 4×4=16 个,分别为(1,1),(1,2),(1,3),(1,4),(2,1)(2,2)(2,3)(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4);
其中满足a-2b+1<0的共有(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(3,3),(3,4),(4,3),(4,4)共10个
故使不等式a-2b+1<0成立的事件发生的概率为:P=
=
,
故选:C
其中满足a-2b+1<0的共有(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(3,3),(3,4),(4,3),(4,4)共10个
故使不等式a-2b+1<0成立的事件发生的概率为:P=
| 10 |
| 16 |
| 5 |
| 8 |
故选:C
点评:本题主要考查等可能事件的概率,满足a-2b+1<0的有10个,是解题的关键.

练习册系列答案
相关题目
下列函数在(1,+∞)上为增函数的是( )
| A、y=-|x-1| | ||
B、y=x+
| ||
C、y=
| ||
| D、y=x(2-x) |
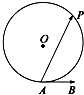 如图,A是半径为5的圆O上的一个定点,单位向量
如图,A是半径为5的圆O上的一个定点,单位向量| AB |
| AP |
| AB |
| A、(-5,5) | ||||
| B、[-5,5] | ||||
C、(-
| ||||
| D、[0,5] |
 如图所示,点M在正六边形ABCDEF的边BC、CD、DE、EF上变动,若
如图所示,点M在正六边形ABCDEF的边BC、CD、DE、EF上变动,若