题目内容
已知中心在原点，长轴在x轴上的椭圆的一个顶点是（0，-
），离心率为
，左、右焦点分别为F1和F2．
（1）求椭圆方程；
（2）试探究椭圆上是否存在一点P，使
•
=0，若存在，请求出点P的坐标；若不存在，请说明理由．
| 5 |
| ||
| 6 |
（1）求椭圆方程；
（2）试探究椭圆上是否存在一点P，使
| PF1 |
| PF2 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：（1）由题意，设椭圆方程为
+
=1，求出a，b即可；
（2）利用三角形的面积推出矛盾，解析几何推方程无解，或者直接利用向量求解．
| x2 |
| a2 |
| y2 |
| b2 |
（2）利用三角形的面积推出矛盾，解析几何推方程无解，或者直接利用向量求解．
解答：
解：（Ⅰ）设椭圆方程为
+
=1．
由已知，b=
，e=
=
．
e2=
=
=1-
，∴1-
=
．
解得a2=6；
∴所求椭圆方程为
+
=1．
（Ⅱ）解法一：假设存在一点P，使
•
=0，
∴
⊥
．
∴△PF1F2为直角三角形，
∴|PF1|2+|PF2|2=|F1F2|2=4①
又∵|PF1|+|PF2|=2a=2
②
∴②2-①，得
2|PF1|•|PF2|=20，
∴
|PF1|•|PF2|=5，
即S△PF1F2=5，但S△PF1F2最大值为
，故矛盾，
∴不存在一点P，使
•
=0．
解法二：假设椭圆上存在一点P，使
•
=0，
则
⊥
，F1（-1，0），F2（1，0），
所以，点P在以F1F2为直径的圆x2+y2=1上，
由
得x2=-24，这是不可能的，
所以椭圆上不存在点P，使
•
=0，
解法三：假设椭圆上存在一点P（x，y），使
•
=0，
则
=(-1-x，-y)，
=(1-x，-y)，
由
•
=0得x2+y2=1，
由
得x2=-24，这是不可能的，
所以椭圆上不存在点P，使
•
=0．
| x2 |
| a2 |
| y2 |
| b2 |
由已知，b=
| 5 |
| c |
| a |
| ||
| 6 |
e2=
| c2 |
| a2 |
| a2-b2 |
| a2 |
| b2 |
| a2 |
| 5 |
| a2 |
| 1 |
| 6 |
解得a2=6；
∴所求椭圆方程为
| x2 |
| 6 |
| y2 |
| 5 |
（Ⅱ）解法一：假设存在一点P，使
| PF1 |
| PF2 |
∴
| PF1 |
| PF2 |
∴△PF1F2为直角三角形，
∴|PF1|2+|PF2|2=|F1F2|2=4①
又∵|PF1|+|PF2|=2a=2
| 6 |
∴②2-①，得
2|PF1|•|PF2|=20，
∴
| 1 |
| 2 |
即S△PF1F2=5，但S△PF1F2最大值为
| 5 |
∴不存在一点P，使
| PF1 |
| PF2 |
解法二：假设椭圆上存在一点P，使
| PF1 |
| PF2 |
则
| PF1 |
| PF2 |
所以，点P在以F1F2为直径的圆x2+y2=1上，
由
|
所以椭圆上不存在点P，使
| PF1 |
| PF2 |
解法三：假设椭圆上存在一点P（x，y），使
| PF1 |
| PF2 |
则
| PF1 |
| PF2 |
由
| PF1 |
| PF2 |
由
|
所以椭圆上不存在点P，使
| PF1 |
| PF2 |
点评：本题考查了椭圆的定义及椭圆中线的关系，同时考查了向量的应用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
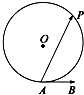如图，A是半径为5的圆O上的一个定点，单位向量| AB |
| AP |
| AB |
| A、（-5，5） | ||||
| B、[-5，5] | ||||
C、(-
| ||||
| D、[0，5] |
函数f（x）=x2-2x-2，x∈[-1，4），则此函数的值域为（ ）
| A、[1，6] |
| B、[1，6 ） |
| C、[-3，6） |
| D、[-3，6] |