题目内容
若关于x的方程|ax-1|=2-a (a>0,且a≠1)有两个不相等的实根,则实数a的取值范围是 .
考点:根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:由题意,关于x的方程|ax-1|=2-a (a>0,且a≠1)有两个不相等的实根,可化为|t-1|=2-a(a>0,且a≠1)有两个不相等的正实根,从而解答.
解答:
解:∵y=ax-1是单调的,
∴关于x的方程|ax-1|=2-a (a>0,且a≠1)有两个不相等的实根,
可化为|t-1|=2-a(a>0,且a≠1)有两个不相等的正实根,
又∵|t-1|=2-a的解为t=1+2-a,或t=1-(2-a),
则有:1+2-a>0,1-(2-a)>0,2-a>0;
解得,1<a<2,
故答案为:(1,2).
∴关于x的方程|ax-1|=2-a (a>0,且a≠1)有两个不相等的实根,
可化为|t-1|=2-a(a>0,且a≠1)有两个不相等的正实根,
又∵|t-1|=2-a的解为t=1+2-a,或t=1-(2-a),
则有:1+2-a>0,1-(2-a)>0,2-a>0;
解得,1<a<2,
故答案为:(1,2).
点评:本题考查了方程根的个数的判断,用到了函数单调性,属于中档题.

练习册系列答案
相关题目
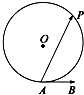 如图,A是半径为5的圆O上的一个定点,单位向量
如图,A是半径为5的圆O上的一个定点,单位向量| AB |
| AP |
| AB |
| A、(-5,5) | ||||
| B、[-5,5] | ||||
C、(-
| ||||
| D、[0,5] |
若1<x<a,则三个数m=logax,n=loga(logax),p=alogax的大小顺序是( )
| A、p<m<n |
| B、p<n<m |
| C、n<m<p |
| D、n<p<m |