题目内容
函数y=log
(x2+4x-1)的单调递增区间是 ..
| 1 |
| 2 |
考点:对数函数的图像与性质
专题:计算题,函数的性质及应用
分析:由题意,x2+4x-1>0,解得,x>
-2或x<-
-2,由复合函数的单调性判断求增区间.
| 5 |
| 5 |
解答:
解:由题意,x2+4x-1>0,
解得,x>
-2或x<-
-2,
又∵y=x2+4x-1在(-∞,-
-2)上是减函数;
在(
-2,+∞)是增函数;
∵y=log
x在(0,+∞)上是减函数,
则函数y=log
(x2+4x-1)的单调递增区间是(-∞,-
-2).
故答案为:(-∞,-
-2).
解得,x>
| 5 |
| 5 |
又∵y=x2+4x-1在(-∞,-
| 5 |
在(
| 5 |
∵y=log
| 1 |
| 2 |
则函数y=log
| 1 |
| 2 |
| 5 |
故答案为:(-∞,-
| 5 |
点评:本题考查了复合函数的单调性的求法,属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
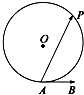 如图,A是半径为5的圆O上的一个定点,单位向量
如图,A是半径为5的圆O上的一个定点,单位向量| AB |
| AP |
| AB |
| A、(-5,5) | ||||
| B、[-5,5] | ||||
C、(-
| ||||
| D、[0,5] |
若1<x<a,则三个数m=logax,n=loga(logax),p=alogax的大小顺序是( )
| A、p<m<n |
| B、p<n<m |
| C、n<m<p |
| D、n<p<m |