题目内容
某建材商场国庆期间搞促销活动,规定:顾客购物总金额不超过800元,不享受任何折扣,如果顾客购物总金额超过800元,超过800元部分享受一定的折扣优惠,按下表折扣分别累计计算:
某人在此商场购物总金额为x元,可以获得的折扣金额为y元.
(1)写出y关于x的解析式.
(2)若y=30,求此人购物实际所付金额.
| 可以享受折扣优惠金额 | 折扣率 |
| 不超过500元的部分 | 5% |
| 超过500元的部分 | 10% |
(1)写出y关于x的解析式.
(2)若y=30,求此人购物实际所付金额.
考点:分段函数的应用
专题:函数的性质及应用
分析:(1)由已知中顾客购物总金额不超过800元,不享受任何折扣,如果顾客购物总金额超过800元,超过800元部分享受95折,如果顾客购物总金额超过1300元,超过1300元部分享受9折,可得到获得的折扣金额y元与购物总金额x元之间的解析式.
(2)根据(1)中函数解析式,结合y=30>25,代入可得某人在此商场购物总金额,减去折扣可得答案.
(2)根据(1)中函数解析式,结合y=30>25,代入可得某人在此商场购物总金额,减去折扣可得答案.
解答:
解:(1)由题可知:
y=
(6分)
(2)∵y=30>25
∴x>1300
∴0.1(x-1300)+25=30
解得,x=1350,
1350-30=1320,
故此人购物实际所付金额为1320元. …(12分)
y=
|
(2)∵y=30>25
∴x>1300
∴0.1(x-1300)+25=30
解得,x=1350,
1350-30=1320,
故此人购物实际所付金额为1320元. …(12分)
点评:本题考查的知识点是分段函数,正确理解题意,进而得到满足条件的分段函数解析式是解答的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
下列函数在(1,+∞)上为增函数的是( )
| A、y=-|x-1| | ||
B、y=x+
| ||
C、y=
| ||
| D、y=x(2-x) |
如直线l1、l2的斜率是二次方程x2-4x+1=0的两根,那么l1与l2的夹角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
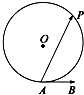 如图,A是半径为5的圆O上的一个定点,单位向量
如图,A是半径为5的圆O上的一个定点,单位向量| AB |
| AP |
| AB |
| A、(-5,5) | ||||
| B、[-5,5] | ||||
C、(-
| ||||
| D、[0,5] |