题目内容
已知数列{an}满足a1=1,an+1=2an+1.
(Ⅰ)证明数列{an+1}是等比数列,并求{an}的通项公式;
(Ⅱ)证明:
+
+…+
<2.
(Ⅰ)证明数列{an+1}是等比数列,并求{an}的通项公式;
(Ⅱ)证明:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)a1=1,an+1=2an+1⇒an+1+1=2(an+1),利用等比数列的定义即可证明数列{an+1}是等比数列,并求得{an}的通项公式;
(Ⅱ)由(Ⅰ)知an=2n-1,易得
<
(n≥2),于是
+
+…+
<1+
+
+…+
=2(1-
)<2.
(Ⅱ)由(Ⅰ)知an=2n-1,易得
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
解答:
证明:(Ⅰ)∵an+1=2an+1,∴an+1+1=2(an+1),
∴{an+1}是以2为首项,2为公比的等比数列,…3分
∴an=2n-1(n∈N*).…5分
(Ⅱ)∵n≥2时(2n-1)-2n-1=2n-1>0,即2n-1>2n-1,
∴
<
(n≥2),…9分
所以
+
+…+
<1+
+
+…+
=2(1-
)<2.…12分
∴{an+1}是以2为首项,2为公比的等比数列,…3分
∴an=2n-1(n∈N*).…5分
(Ⅱ)∵n≥2时(2n-1)-2n-1=2n-1>0,即2n-1>2n-1,
∴
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
所以
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
点评:本题考查等比关系的确定,突出考查放缩法的应用,考查逻辑推理与证明的能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=(x-a)(x-b),(a>b)的图象如图所示,则g(x)=ax+b的图象经过( )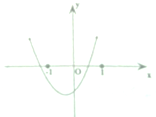

| A、第一、二、三象限 |
| B、第一、二、四象限 |
| C、第一、三、四象限 |
| D、第二、三、四象限 |
在区间[0,1]上随机取一个数x,使y=3x-1的值介于1与2之间的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|