题目内容

已知函数f（x）=（x-a）（x-b），（a＞b）的图象如图所示，则g（x）=ax+b的图象经过（　　）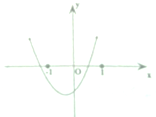
A、第一、二、三象限
B、第一、二、四象限
C、第一、三、四象限
D、第二、三、四象限
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：由已知中函数f（x）=（x-a）（x-b）的图象可得：0＜a＜1，b＜-1，进而结合指数函数的图象和性质及函数图象的平移变换法则，画出g（x）=ax+b的图象，可得答案．
解答： 解：由已知中函数f（x）=（x-a）（x-b）的图象可得：
0＜a＜1，b＜-1，
故g（x）=ax+b的图象如下图所示：

由图可知，函数的图象经过二，三，四象限，
故选：D
点评：本题考查的知识点是指数函数的图象和性质，其中根据已知分析出0＜a＜1，b＜-1，是解答的关键．
练习册系列答案
相关题目
设f（x）=
x2
x+1
，g（x）=ax+5-2a（a＞0）．
（1）求f（x）在区间[0，1]上的值域；
（2）若对于任意x1∈[0，1]，总存在x2∈[0，1]，使得g（x2）-f（x1）＜0成立，求实数a的取值范围．
已知函数y=f（x）与函数y=cosx有相同的奇偶性，与函数y=tanx有相同的周期，在[
π
2
，π]上与函数y=sinx有相同的图象，
①f（
4π
3
）=-
3
2
；
②函数y=f（x）的图象的对称轴为x=
kπ
2
，k∈Z；
③函数y=f（x）值域是[-1，1]；
④函数y=f（x）的单调增区间是[kπ，kπ+
π
2
]，k∈Z．
则以上说法正确的序号是
 
．
在矩形ABCD中，AD=2AB，点E为AD的中点，则cos∠EBD=（　　）
A、
3
2
B、
3
3
C、
10
5
D、
3
10
10
已知x=lnπ，y=lg3，z=log3π，则（　　）
A、z＜y＜x
B、z＜x＜y
C、y＜z＜x
D、y＜x＜z
下列函数中，既是奇函数又在（0，+∞）上单调递减的函数是（　　）
A、y=
1
x
B、y=e-x
C、y=-tanx
D、y=|x|
已知数列{an}满足a1=1，an+1=2an+1．
（Ⅰ）证明数列{an+1}是等比数列，并求{an}的通项公式；
（Ⅱ）证明：
1
a1
+
1
a2
+…+
1
an
＜2．
已知定义在（-∞，0）∪（0，+∞）上的函数f（x）满足f（-x）=f（x），当a，b∈（-∞，0）时总有
f(a)-f(b)
a-b
＞0（a≠b），若f（m+1）＞f（2m），则实数m的取值范围是
 
．
已知函数f（x）=loga
1+x
1-x
（a＞0，a≠1）
（1）求定义域．
（2）判断奇偶性并证明．
（3）当a＞1时，函数f（x）在定义域上是
 
（填增减性，不必说明理由．）
（4）当0＜a＜1时，求使f（x）＞0的x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网