题目内容

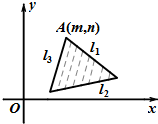已知约束条件对应的平面区域D如图所示，其中l1，l2，l3对应的直线方程分别为：y=k1x+b1，y=k2x+b2，y=k3x+b3，若目标函数z=-kx+y仅在点A（m，n）处取到最大值，则有（　　）
A、k1＜k＜k2
B、k1＜k＜k3
C、k1≤k≤k3
D、k＜k1或k＞k3
考点：简单线性规划
专题：不等式的解法及应用
分析：根据z的几何意义，结合直线斜率之间的关系，即可得到结论．
解答： 解：A是l1与l3的交点，目标函数z=-kx+y仅在点A处取到最大值，
∴直线y=kx+z的倾斜角比l1的要大，比l3的要小，
即有k1＜k＜k3，
故选：B．
点评：本题主要考查线性规划的应用以及直线斜率之间的关系，比较基础．
练习册系列答案
相关题目
已知命题“若点M（x0，y0）是圆x2+y2=r2上一点，则过点M的圆的切线方程为x0x+y0y=r2”．
（Ⅰ）根据上述命题类比：“若点M（x0，y0）是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上一点，则过点M的切线方程为
 
”（写出直线的方程，不必证明）．
（Ⅱ）已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左焦点为F1（-1，0），且经过点（1，
3
2
）．
（i）求椭圆C的方程；
（ii）过F1的直线l交椭圆C于A、B两点，过点A、B分别作椭圆的两条切线，求其交点的轨迹方程．
如图3，AB是圆O的直径，PB、PD是圆O的切线，切点为B、C，∠ACD=30°．则
PC
AC
=
 
．
已知sin（α+
π
4
）=
1
2
，则sin2α=
 
．
若不等式x2-2x+3-a＜0成立的一个充分条件是0＜x＜4，则实数a的取值范围应为（　　）
A、a≥11B、a＞11
C、a＞9D、a≥9
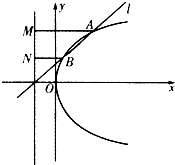如图，已知直线l：y=k（x+1）（k＞0）与抛物线C：y2=4x相交于A、B两点，且A、B两点在抛物线C准线上的射影分别是M、N，若|AM|=2|BN|，则k的值是（　　）
A、
1
3
B、
2
3
C、
2
3
2
D、2
2
阅读如图所示的程序框图，运行相应的程序，输出的结果i=（　　）
A、3B、4C、5D、6
已知x，y满足
x≥1
x+y≤4
x-y-2≤0
，则z=2x+y的最大值是（　　）
A、1B、5C、7D、9
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，以原点为圆心，椭圆的短半轴长为半径的圆与直线x-y+
2
=0相切．
（1）求椭圆C的方程；
（2）若过点M（2，0）的直线与椭圆C相交于两点A，B，以OA，OB为邻边作一个平行四边形OAQB，记直线OQ与椭圆交于P点，且满足
|OQ|
|OP|
=λ（O为坐标原点），求实数λ的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网