题目内容
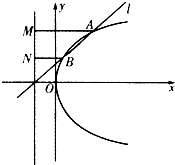 如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是( )
如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
考点:直线与圆锥曲线的综合问题
专题:空间向量及应用
分析:直线y=k(x+1)(k>0)恒过定点P(-1,0),由此推导出|OB|=
|AF|,由此能求出点B的坐标,从而能求出k的值.
| 1 |
| 2 |
解答:
解:设抛物线C:y2=4x的准线为l:x=-1
直线y=k(x+1)(k>0)恒过定点P(-1,0)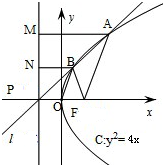
如图过A、B分别作AM⊥l于M,BN⊥l于N,
由|FA|=2|FB|,则|AM|=2|BN|,
点B为AP的中点、连接OB,
则|OB|=
|AF|,
∴|OB|=|BF|,点B的横坐标为
,
∴点B的坐标为B(
,
),
把B(
,
)代入直线l:y=k(x+1)(k>0),
解得k=
.
故选:C.
直线y=k(x+1)(k>0)恒过定点P(-1,0)

如图过A、B分别作AM⊥l于M,BN⊥l于N,
由|FA|=2|FB|,则|AM|=2|BN|,
点B为AP的中点、连接OB,
则|OB|=
| 1 |
| 2 |
∴|OB|=|BF|,点B的横坐标为
| 1 |
| 2 |
∴点B的坐标为B(
| 1 |
| 2 |
| 2 |
把B(
| 1 |
| 2 |
| 2 |
解得k=
| 2 |
| 3 |
| 2 |
故选:C.
点评:本题考查直线与圆锥曲线中参数的求法,考查抛物线的性质,是中档题,解题时要注意等价转化思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若点(x,y)在曲线y=-|x|与y=-2所围成的封闭区域内(包括边界),则2x-y的最大值为( )
| A、-6 | B、4 | C、6 | D、8 |
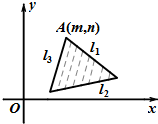 已知约束条件对应的平面区域D如图所示,其中l1,l2,l3对应的直线方程分别为:y=k1x+b1,y=k2x+b2,y=k3x+b3,若目标函数z=-kx+y仅在点A(m,n)处取到最大值,则有( )
已知约束条件对应的平面区域D如图所示,其中l1,l2,l3对应的直线方程分别为:y=k1x+b1,y=k2x+b2,y=k3x+b3,若目标函数z=-kx+y仅在点A(m,n)处取到最大值,则有( )| A、k1<k<k2 |
| B、k1<k<k3 |
| C、k1≤k≤k3 |
| D、k<k1或k>k3 |
下列命题中,真命题是( )
| A、命题“若p,则q”的否命题是“若p,则¬q” | ||
B、a+b=0的充要条件是
| ||
| C、已知命题p、q,若“p∨q”为假命题,则命题p与q一真一假 | ||
| D、命题p:?x∈R,使得x2+1<0,则¬p:?x∈R,使得x2+1≥0 |
定义在R上的奇函数f(x)满足f(x-2)=-f(x),且在[0,1]上是增函数,则有( )
A、f(
| ||||||
B、f(-
| ||||||
C、f(
| ||||||
D、f(-
|