题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+
=0相切.
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A,B,以OA,OB为邻边作一个平行四边形OAQB,记直线OQ与椭圆交于P点,且满足
=λ(O为坐标原点),求实数λ的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A,B,以OA,OB为邻边作一个平行四边形OAQB,记直线OQ与椭圆交于P点,且满足
| |OQ| |
| |OP| |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用椭圆的离心率为
,求出a,b的关系,结合以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+
=0相切,求出a,b的值,即可得出结论;
(2)设AB:y=k(x-2),直线代入椭圆方程,利用韦达定理,确定Q的中点,进而可得P的坐标,代入椭圆方程,即可得出结论.
| ||
| 2 |
| 2 |
(2)设AB:y=k(x-2),直线代入椭圆方程,利用韦达定理,确定Q的中点,进而可得P的坐标,代入椭圆方程,即可得出结论.
解答:
解:(1)由题意知椭圆的离心率为
,∴
=
,即a2=2b2
又∵以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+
=0相切
∴b=
=1,
∴a2=2,b2=1.
故椭圆C的方程为
+y2=1;
(2)由题意知直线AB的斜率存在.
设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),
直线代入椭圆方程可得(1+2k2)x2-8k2x+8k2-2=0
△=64k4-4(2k2+1)(8k2-2)>0,∴k2<
,
x1+x2=
,x1x2=
.
∴AB的中点为(
,
),
∴Q(
,
),
∵
=λ,
∴x=
•
,y=
•
,
代入椭圆方程可得λ=
=
,
∵k2<
,
∴
+2k>3或
+2k<-3,
∴0<
<
或-
<
<0,
∴0<λ<
或-
<λ<0.
| ||
| 2 |
| a2-b2 |
| a2 |
| 1 |
| 2 |
又∵以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+
| 2 |
∴b=
| ||
|
∴a2=2,b2=1.
故椭圆C的方程为
| x2 |
| 2 |
(2)由题意知直线AB的斜率存在.
设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),
直线代入椭圆方程可得(1+2k2)x2-8k2x+8k2-2=0
△=64k4-4(2k2+1)(8k2-2)>0,∴k2<
| 1 |
| 2 |
x1+x2=
| 8k2 |
| 1+2k2 |
| 8k2-2 |
| 1+2k2 |
∴AB的中点为(
| 4k2 |
| 1+2k2 |
| -2k |
| 1+2k2 |
∴Q(
| 8k2 |
| 1+2k2 |
| -4k |
| 1+2k2 |
∵
| |OQ| |
| |OP| |
∴x=
| 1 |
| λ |
| 8k2 |
| 1+2k2 |
| 1 |
| λ |
| -4k |
| 1+2k2 |
代入椭圆方程可得λ=
| 4k |
| 1+2k2 |
| 4 | ||
|
∵k2<
| 1 |
| 2 |
∴
| 1 |
| k |
| 1 |
| k |
∴0<
| 4 | ||
|
| 4 |
| 3 |
| 4 |
| 3 |
| 4 | ||
|
∴0<λ<
| 4 |
| 3 |
| 4 |
| 3 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于难题.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
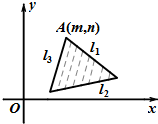 已知约束条件对应的平面区域D如图所示,其中l1,l2,l3对应的直线方程分别为:y=k1x+b1,y=k2x+b2,y=k3x+b3,若目标函数z=-kx+y仅在点A(m,n)处取到最大值,则有( )
已知约束条件对应的平面区域D如图所示,其中l1,l2,l3对应的直线方程分别为:y=k1x+b1,y=k2x+b2,y=k3x+b3,若目标函数z=-kx+y仅在点A(m,n)处取到最大值,则有( )| A、k1<k<k2 |
| B、k1<k<k3 |
| C、k1≤k≤k3 |
| D、k<k1或k>k3 |
已知i是虚数单位,若
=1-i,则z的共轭复数为( )
| 3+i |
| z |
| A、1-2i | ||||
| B、2-4i | ||||
C、
| ||||
| D、1+2i |
 如图,椭圆C的中心为原点O,长轴在x轴上,离心率e=
如图,椭圆C的中心为原点O,长轴在x轴上,离心率e=