题目内容
已知sin(α+
)=
,则sin2α= .
| π |
| 4 |
| 1 |
| 2 |
考点:二倍角的正弦
专题:三角函数的求值
分析:由sin(α+
)=
(sinα+cosα)=
求得sinα+cosα=
,平方求得sin2α的值.
| π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解答:
解:由sin(α+
)=
(sinα+cosα)=
可得sinα+cosα=
,
平方可得 sin2α=-
.
故答案为:-
.
| π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
平方可得 sin2α=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题主要考查两角和的正弦公式、二倍角公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若点(x,y)在曲线y=-|x|与y=-2所围成的封闭区域内(包括边界),则2x-y的最大值为( )
| A、-6 | B、4 | C、6 | D、8 |
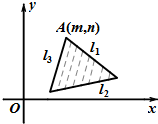 已知约束条件对应的平面区域D如图所示,其中l1,l2,l3对应的直线方程分别为:y=k1x+b1,y=k2x+b2,y=k3x+b3,若目标函数z=-kx+y仅在点A(m,n)处取到最大值,则有( )
已知约束条件对应的平面区域D如图所示,其中l1,l2,l3对应的直线方程分别为:y=k1x+b1,y=k2x+b2,y=k3x+b3,若目标函数z=-kx+y仅在点A(m,n)处取到最大值,则有( )| A、k1<k<k2 |
| B、k1<k<k3 |
| C、k1≤k≤k3 |
| D、k<k1或k>k3 |
定义在R上的奇函数f(x)满足f(x-2)=-f(x),且在[0,1]上是增函数,则有( )
A、f(
| ||||||
B、f(-
| ||||||
C、f(
| ||||||
D、f(-
|
 如图,椭圆C的中心为原点O,长轴在x轴上,离心率e=
如图,椭圆C的中心为原点O,长轴在x轴上,离心率e=