题目内容
已知命题“若点M(x0,y0)是圆x2+y2=r2上一点,则过点M的圆的切线方程为x0x+y0y=r2”.
(Ⅰ)根据上述命题类比:“若点M(x0,y0)是椭圆
+
=1(a>b>0)上一点,则过点M的切线方程为 ”(写出直线的方程,不必证明).
(Ⅱ)已知椭圆C:
+
=1(a>b>0)的左焦点为F1(-1,0),且经过点(1,
).
(i)求椭圆C的方程;
(ii)过F1的直线l交椭圆C于A、B两点,过点A、B分别作椭圆的两条切线,求其交点的轨迹方程.
(Ⅰ)根据上述命题类比:“若点M(x0,y0)是椭圆
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅱ)已知椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
(i)求椭圆C的方程;
(ii)过F1的直线l交椭圆C于A、B两点,过点A、B分别作椭圆的两条切线,求其交点的轨迹方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)仿照圆的切线方程进行类比,能求出过椭圆上一点的切线方程.
(Ⅱ)(ⅰ)设椭圆C:
+
=1,把点(1,
)代入,能求出椭圆方程.
(ⅱ)分别求出椭圆在点A、B处的切线方程,联立方程组能求出交点的轨迹方程.
(Ⅱ)(ⅰ)设椭圆C:
| x2 |
| a2 |
| y2 |
| a2-1 |
| 3 |
| 2 |
(ⅱ)分别求出椭圆在点A、B处的切线方程,联立方程组能求出交点的轨迹方程.
解答:
解:(Ⅰ)
+
=1.(3分)
(Ⅱ)(ⅰ)∵椭圆C:
+
=1(a>b>0)的左焦点F1(-1,0),
∴设椭圆C:
+
=1,
∵椭圆经过点(1,
),
∴
+
=1,
整理,得4a4-17a2+4=0,
解得a2=4,或a2=
,
∴椭圆方程为:
+
=1.(7分)
(ⅱ)当直线l的斜率存在时,设为k,直线l的方程为y=k(x+1),
设A(x1,y1),B(x2,y2),
则椭圆在点A处的切线方程为:
+
=1,①
椭圆在点B的切线方程为:
+
=1,②
联立方程①②得:x=
=
=-4,
即此时交点的轨迹方程:x=4.(11分)
当直线l的斜率不存在时,直线l的方程为x=-1,
此时A(-1,
),B(-1,-
),经过AB两点的切线交点为(-4,0).
综上所述,切线的交点的轨迹方程为:x=-4.(13分)
| x0x |
| a2 |
| y0y |
| b2 |
(Ⅱ)(ⅰ)∵椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
∴设椭圆C:
| x2 |
| a2 |
| y2 |
| a2-1 |
∵椭圆经过点(1,
| 3 |
| 2 |
∴
| 1 |
| a2 |
| 9 |
| 4a2-4 |
整理,得4a4-17a2+4=0,
解得a2=4,或a2=
| 1 |
| 4 |
∴椭圆方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(ⅱ)当直线l的斜率存在时,设为k,直线l的方程为y=k(x+1),
设A(x1,y1),B(x2,y2),
则椭圆在点A处的切线方程为:
| x1x |
| 4 |
| y1y |
| 3 |
椭圆在点B的切线方程为:
| x2x |
| 4 |
| y2y |
| 3 |
联立方程①②得:x=
| 4(y2-y1) |
| x1y2-x2y1 |
| 4k(x2-x1) |
| x1k(x2-1)-x2k(x1+1) |
即此时交点的轨迹方程:x=4.(11分)
当直线l的斜率不存在时,直线l的方程为x=-1,
此时A(-1,
| 3 |
| 2 |
| 3 |
| 2 |
综上所述,切线的交点的轨迹方程为:x=-4.(13分)
点评:本题考查切线方程的求法,考查椭圆方程的求法,考查交点的轨迹方程的求法,解题时要认真审题,注意计算能力、推理论证能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
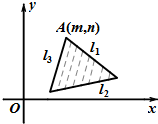 已知约束条件对应的平面区域D如图所示,其中l1,l2,l3对应的直线方程分别为:y=k1x+b1,y=k2x+b2,y=k3x+b3,若目标函数z=-kx+y仅在点A(m,n)处取到最大值,则有( )
已知约束条件对应的平面区域D如图所示,其中l1,l2,l3对应的直线方程分别为:y=k1x+b1,y=k2x+b2,y=k3x+b3,若目标函数z=-kx+y仅在点A(m,n)处取到最大值,则有( )| A、k1<k<k2 |
| B、k1<k<k3 |
| C、k1≤k≤k3 |
| D、k<k1或k>k3 |
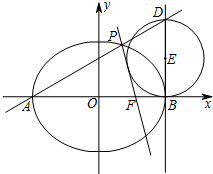 已知椭圆C的中心在坐标原点,右焦点为F(1,0),A、B是椭圆C的左、右顶点,P是椭圆C上异于A、B的动点,且△APB面积的最大值为2
已知椭圆C的中心在坐标原点,右焦点为F(1,0),A、B是椭圆C的左、右顶点,P是椭圆C上异于A、B的动点,且△APB面积的最大值为2