题目内容
如图3,AB是圆O的直径,PB、PD是圆O的切线,切点为B、C,∠ACD=30°.则
= .
| PC |
| AC |

考点:与圆有关的比例线段
专题:直线与圆
分析:连结OC,由题设条件推导出∠AOC=2∠ACD=60°,∠PCO=90°,∠POC=60°,∠OPC=30°,由此能求出
的值.
| PC |
| AC |
解答:
解: 连结OC,
连结OC,
∵AB是圆O的直径,PB、PD是圆O的切线,切点为B、C,∠ACD=30°,
∴∠AOC=2∠ACD=60°,∠PCO=90°,
∴∠POC=60°,∠OPC=30°,
设OC=a,则AC=OC=a,OP=2a,PC=
=
a,
∴
=
=
.
故答案为:
.
 连结OC,
连结OC,∵AB是圆O的直径,PB、PD是圆O的切线,切点为B、C,∠ACD=30°,
∴∠AOC=2∠ACD=60°,∠PCO=90°,
∴∠POC=60°,∠OPC=30°,
设OC=a,则AC=OC=a,OP=2a,PC=
| (2a)2-a2 |
| 3 |
∴
| PC |
| AC |
| ||
| a |
| 3 |
故答案为:
| 3 |
点评:本题考查与圆有关的两条线段的比值的求法,是中档题,解题时要注意弦切角定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
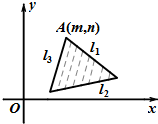 已知约束条件对应的平面区域D如图所示,其中l1,l2,l3对应的直线方程分别为:y=k1x+b1,y=k2x+b2,y=k3x+b3,若目标函数z=-kx+y仅在点A(m,n)处取到最大值,则有( )
已知约束条件对应的平面区域D如图所示,其中l1,l2,l3对应的直线方程分别为:y=k1x+b1,y=k2x+b2,y=k3x+b3,若目标函数z=-kx+y仅在点A(m,n)处取到最大值,则有( )| A、k1<k<k2 |
| B、k1<k<k3 |
| C、k1≤k≤k3 |
| D、k<k1或k>k3 |
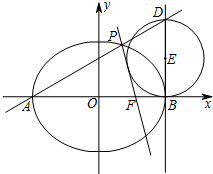 已知椭圆C的中心在坐标原点,右焦点为F(1,0),A、B是椭圆C的左、右顶点,P是椭圆C上异于A、B的动点,且△APB面积的最大值为2
已知椭圆C的中心在坐标原点,右焦点为F(1,0),A、B是椭圆C的左、右顶点,P是椭圆C上异于A、B的动点,且△APB面积的最大值为2