题目内容
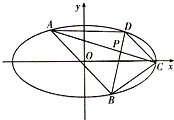 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| AP |
| PC |
| BP |
| PD |
(1)求椭圆的方程;
(2)求直线AB的斜率.
考点:椭圆的标准方程,直线的一般式方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用椭圆
+
=1(a>b>0)过点(1,
),离心率为
,建立方程,求出a,b,即可求椭圆的方程;
(2)确定C的坐标,代入椭圆方程,整理可得x1+y1=-
,同理可得x2+y2=-
,两试相减,即可求直线AB的斜率.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
(2)确定C的坐标,代入椭圆方程,整理可得x1+y1=-
| 1 |
| 8 |
| 1 |
| 8 |
解答:
解:(1)∵椭圆
+
=1(a>b>0)过点(1,
),离心率为
,
∴
=
,
+
=1
∴a=2,b=1,
∴椭圆的方程为
+y2=1;
(2)设A(x1,y1),B(x2,y2),
∵
=2
,∴C(
,
),
代入椭圆方程,整理可得x1+y1=-
①,
同理可得x2+y2=-
②,
①-②,可得直线AB的斜率为-1.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
∴
| c |
| a |
| ||
| 2 |
| 1 |
| a2 |
| ||
| b2 |
∴a=2,b=1,
∴椭圆的方程为
| x2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),
∵
| AP |
| PC |
| 3-x1 |
| 2 |
| 3-4y1 |
| 8 |
代入椭圆方程,整理可得x1+y1=-
| 1 |
| 8 |
同理可得x2+y2=-
| 1 |
| 8 |
①-②,可得直线AB的斜率为-1.
点评:本题考查椭圆方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
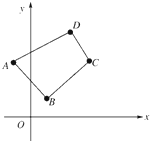 已知四点坐标:A(-1,3),B(1,1),C(4,4),D(3,5).
已知四点坐标:A(-1,3),B(1,1),C(4,4),D(3,5). 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(即六组)[40,50),[50,60),…[90,100]后,画出如图部分频率分布直方图.请根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(即六组)[40,50),[50,60),…[90,100]后,画出如图部分频率分布直方图.请根据图形的信息,回答下列问题: