题目内容
 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(即六组)[40,50),[50,60),…[90,100]后,画出如图部分频率分布直方图.请根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(即六组)[40,50),[50,60),…[90,100]后,画出如图部分频率分布直方图.请根据图形的信息,回答下列问题:(1)求第四小组的频率并在图中将频率直方图补充完整;
(2)估计这次考试成绩的中位数和及格率(60分及以上为及格);
(3)用分层抽样的方法从成绩在[40,50)和[70,80]的学生中共抽取4人,在抽出的4人中任取2人,求成绩在[40,50)和[70,80]中各有1人的概率.
考点:频率分布直方图,古典概型及其概率计算公式
专题:概率与统计
分析:(1)由频率分布的直方图可得,第四小组的频率等于1减去其它小组的频率,第四个小矩形的高等于频率除以组距.
(2)这次考试的及格的频率等于60分以上各个组的频率之和,此值即为及格的概率.用各个组的平均值乘以该组的频率,即得所求的平均分.
(3)由频率分步直方图可得,成绩是40~50分的有6人,90~100分的学生有18人,从中抽取4人,则两组分别抽取1人和3人,求出在抽出的4人中任取2人,和成绩在[40,50)和[70,80]中各有1人的抽取方法数,代入古典概型概率计算公式,可得答案.
(2)这次考试的及格的频率等于60分以上各个组的频率之和,此值即为及格的概率.用各个组的平均值乘以该组的频率,即得所求的平均分.
(3)由频率分步直方图可得,成绩是40~50分的有6人,90~100分的学生有18人,从中抽取4人,则两组分别抽取1人和3人,求出在抽出的4人中任取2人,和成绩在[40,50)和[70,80]中各有1人的抽取方法数,代入古典概型概率计算公式,可得答案.
解答:
解:(1)由频率分布的直方图可得,第四小组的频率为 1-10(0.01+0.015+0.015+0.025+0.05)=0.3.
故第四个小矩形的高为
=0.03.如图所示:

(2)由于这次考试的及格的频率为10×(0.015+0.03+0.025+0.005)=0.75,故及格率为0.75.
由前三组累积频率0.4,前四组累积频率0.7,故中位数在第四组,
设中位数为70+x.则
=
,
解得x=
故中位数估计为:
(3)由频率分步直方图可得,成绩是40~50分的有60×0.1=6人,70~80分的学生有60×0.3=18人,
从成绩在[40,50)和[70,80]的学生中共抽取4人,则在[40,50)和[70,80]分别抽取1人,3人,
从中任取2人,共有6种情况,
其中成绩在[40,50)和[70,80]中各有1人有3种情况,
故成绩在[40,50)和[70,80]中各有1人的概率P=
=
故第四个小矩形的高为
| 0.3 |
| 10 |

(2)由于这次考试的及格的频率为10×(0.015+0.03+0.025+0.005)=0.75,故及格率为0.75.
由前三组累积频率0.4,前四组累积频率0.7,故中位数在第四组,
设中位数为70+x.则
| x |
| 10 |
| 1 |
| 3 |
解得x=
| 10 |
| 3 |
故中位数估计为:
| 220 |
| 3 |
(3)由频率分步直方图可得,成绩是40~50分的有60×0.1=6人,70~80分的学生有60×0.3=18人,
从成绩在[40,50)和[70,80]的学生中共抽取4人,则在[40,50)和[70,80]分别抽取1人,3人,
从中任取2人,共有6种情况,
其中成绩在[40,50)和[70,80]中各有1人有3种情况,
故成绩在[40,50)和[70,80]中各有1人的概率P=
| 3 |
| 6 |
| 1 |
| 2 |
点评:本题主要考查频率分步直方图,古典概型及其概率计算公式的应用,属于基础题.

练习册系列答案
相关题目

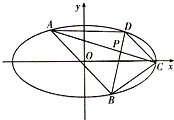 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆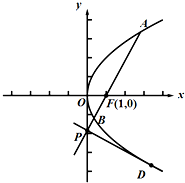 抛物线C:y2=2px(p>0),过抛物线C的焦点F(1,0)的直线l与抛物线交于A,B两点,交y轴于点P.
抛物线C:y2=2px(p>0),过抛物线C的焦点F(1,0)的直线l与抛物线交于A,B两点,交y轴于点P.