题目内容
已知两点A(-2,-2),B(-4,0),直线l:y=kx+2.
(1)直线AB⊥l,求k的值;
(2)直线 l与线段AB有交点,求k的取值范围;
(3)直线 l截以AB为直径的圆所得弦长为
,求k的值.
(1)直线AB⊥l,求k的值;
(2)直线 l与线段AB有交点,求k的取值范围;
(3)直线 l截以AB为直径的圆所得弦长为
2
| ||
| 5 |
考点:两条直线的交点坐标
专题:直线与圆
分析:(1)由两点求斜率得到AB所在直线的斜率,结合两直线垂直得答案;
(2)数形结合求得使直线 l与线段AB有交点的k的取值范围;
(3)写出以AB为直径的圆的方程,求出圆心到直线的距离,结合弦长为
列式求k的值.
(2)数形结合求得使直线 l与线段AB有交点的k的取值范围;
(3)写出以AB为直径的圆的方程,求出圆心到直线的距离,结合弦长为
2
| ||
| 5 |
解答:
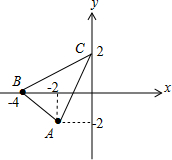 解:(1)A(-2,-2),B(-4,0),
解:(1)A(-2,-2),B(-4,0),
∴kAB=
=-1,
∵直线AB⊥l,
∴k=1;
(2)如图,
直线l:y=kx+2过定点C(0,2),
kAC=
=2,kBC=
=
.
∴k∈[
,2];
(3)以AB为直径的圆为(x+3)2+(y+1)2=2,
d=
=
=
,
∴12k2-25k+12=0,
解得:k=
或k=
.
 解:(1)A(-2,-2),B(-4,0),
解:(1)A(-2,-2),B(-4,0),∴kAB=
| -2-0 |
| -2-(-4) |
∵直线AB⊥l,
∴k=1;
(2)如图,
直线l:y=kx+2过定点C(0,2),
kAC=
| -2-2 |
| -2 |
| 0-2 |
| -4-0 |
| 1 |
| 2 |
∴k∈[
| 1 |
| 2 |
(3)以AB为直径的圆为(x+3)2+(y+1)2=2,
d=
| |-3k+3| | ||
|
2-(
|
| 3 |
| 5 |
∴12k2-25k+12=0,
解得:k=
| 4 |
| 3 |
| 3 |
| 4 |
点评:本题考查了直线的斜率,考查了数形结合的解题思想方法,考查了直线与圆的关系,是中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
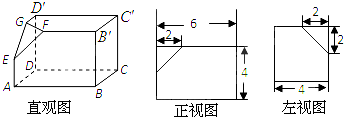

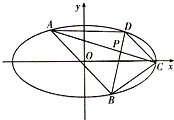 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆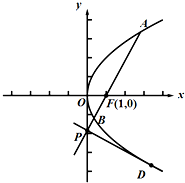 抛物线C:y2=2px(p>0),过抛物线C的焦点F(1,0)的直线l与抛物线交于A,B两点,交y轴于点P.
抛物线C:y2=2px(p>0),过抛物线C的焦点F(1,0)的直线l与抛物线交于A,B两点,交y轴于点P. 中国首届绿色运动会2011年10月18日至11月2日在安徽池州举行.绿运会期间,“上海城”举办了绿色产品展销会,并在展销会场设有购物满50元就获得一次有奖摸球活动.一个不透明的袋子中装有大小相同的8个球,其中标有1,2,3,4数字的球各2个,现从中任意抽取2个,用ξ表示抽取的这两个球上的数字之和.求:
中国首届绿色运动会2011年10月18日至11月2日在安徽池州举行.绿运会期间,“上海城”举办了绿色产品展销会,并在展销会场设有购物满50元就获得一次有奖摸球活动.一个不透明的袋子中装有大小相同的8个球,其中标有1,2,3,4数字的球各2个,现从中任意抽取2个,用ξ表示抽取的这两个球上的数字之和.求: