题目内容

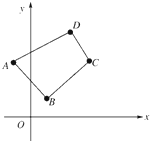已知四点坐标：A（-1，3），B（1，1），C（4，4），D（3，5）．
（1）求证：四边形ABCD是直角梯形；
（2）求cos∠DAB的值．
考点：平面向量的坐标运算
专题：平面向量及应用
分析：（1）利用向量的垂直与数量积的关系即可得出；
（2）利用向量的夹角公式即可得出．
解答： 解：（1）
AB
=（2，-2），
BC
=（3，3），
CD
=（-1，1），
AD
=（4，2）．
∴
AB
•
BC
=0，
BC
•
CD
=0，
AB
•
AD
≠0．
∴
AB
⊥
BC
，
BC
⊥
CD
，
∴AB∥CD．
∴四边形ABCD是直角梯形；
（2）cos∠DAB=
AD
•
AB
|
AD
||
AB
|
=
4
8
•
20
=
10
10
．
点评：本题考查了向量的垂直与数量积的关系、向量的夹角公式，属于基础题．
练习册系列答案
相关题目
已知
a
=（sinωx，
3
sinωx），
b
=（sinωx，cosωx），ω＞0，f（x）=
a
•
b
，且f（x）的最小正周期为π．
（1）求f（x）的单调递减区间．
（2）求f（x）在区间[0，
2π
3
]上的取值范围．
（1）计算
lg2+lg5-lg8
lg50-lg40
；
（2）设3a=4b=36，求
2
a
+
1
b
的值．
若a+a-1=3，求a 
1
2
-a -
1
2
及a2+a-2的值．
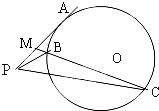如图，PA是圆O的切线，切点为A，过PA的中点M作割线交圆O于点B和C．
求证：∠MPB=∠MCP．
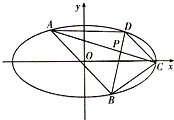 如图，在平面直角坐标系xOy中，椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）过点（1，
3
2
），离心率为
3
2
，又椭圆内接四边形ABCD（点A、B、C、D在椭圆上）的对角线AC，BD相交于点P（1，
1
4
），且
AP
=2
PC
，
BP
=2
PD
．
（1）求椭圆的方程；
（2）求直线AB的斜率．
某研究性学习小组对昼夜温差与某种子发芽数的关系进行研究，他们分别记录了四天中每天昼夜温差与每天100粒种子浸泡后的发芽数，得到如下资料：
时间第一天第二天第三天第四天
温差（℃）910811
发芽（粒）33392646
（1）求这四天浸泡种子的平均发芽率；
（2）有这样一个研究项目，在这四天中任选两天，记发芽的种子数分别为m，n（m＜n），请以（m，n）的形式列出所有的基本事件，记事件A为“m，n满足
m＞30
n＞40
”，求事件A发生的概率．
设函数f（x）的定义域为R，对任意实数x、y都有f（x+y）=f（x）+f（y），当x＞0时f（x）＞0且f（2）=6．
（1）求证：函数f（x）为奇函数；
（2）证明函数f（x）在R上是增函数；
（3）在区间[-4，4]上，求f（x）的最值．
两个非零向量
a
与
b
满足|
a
|=4，|
b
|=2，且
a
与
b
夹角为60°．
（1）求
a
•
b
；
（2）|
a
+
b
|．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网