题目内容
Rt△ABC的三边长分别是AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得到的旋转体的表面积和体积.
考点:旋转体(圆柱、圆锥、圆台),棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:利用等面积求出OC,再求所得到的旋转体的表面积和体积.
解答:
 解:如图,旋转后图形的轴截面是四边形ACBC',
解:如图,旋转后图形的轴截面是四边形ACBC',
连结CC'交AB于O,则CC'⊥AB
∵AC=3,BC=4,AB=5
∴AB2=AC2+BC2,
∴△ABC是直角三角形,
∴S△ABC=
AB×OC=
AC×BC
∴OC=2.4,
∴旋转体的体积=两个圆锥体积和=
×π×2.42×AB=
旋转体的表面积=
×2π×2.4×(3+4)=
 解:如图,旋转后图形的轴截面是四边形ACBC',
解:如图,旋转后图形的轴截面是四边形ACBC',连结CC'交AB于O,则CC'⊥AB
∵AC=3,BC=4,AB=5
∴AB2=AC2+BC2,
∴△ABC是直角三角形,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴OC=2.4,
∴旋转体的体积=两个圆锥体积和=
| 1 |
| 3 |
| 48π |
| 5 |
旋转体的表面积=
| 1 |
| 2 |
| 84π |
| 5 |
点评:本题考查旋转体的表面积和体积,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
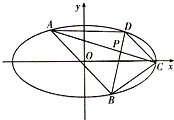 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆 中国首届绿色运动会2011年10月18日至11月2日在安徽池州举行.绿运会期间,“上海城”举办了绿色产品展销会,并在展销会场设有购物满50元就获得一次有奖摸球活动.一个不透明的袋子中装有大小相同的8个球,其中标有1,2,3,4数字的球各2个,现从中任意抽取2个,用ξ表示抽取的这两个球上的数字之和.求:
中国首届绿色运动会2011年10月18日至11月2日在安徽池州举行.绿运会期间,“上海城”举办了绿色产品展销会,并在展销会场设有购物满50元就获得一次有奖摸球活动.一个不透明的袋子中装有大小相同的8个球,其中标有1,2,3,4数字的球各2个,现从中任意抽取2个,用ξ表示抽取的这两个球上的数字之和.求: