题目内容
抛物线y2=2px(p>0)上的点T(3,t)到焦点F的距离为4.
(1)求
的值;
(2)设抛物线的准线与x轴的交点为M.问:是否存在过M的直线l交抛物线于A、B(B在A的右侧)两点,使得直线AF⊥OB?若存在,求出△AFB的面积.
(1)求
| t |
| p |
(2)设抛物线的准线与x轴的交点为M.问:是否存在过M的直线l交抛物线于A、B(B在A的右侧)两点,使得直线AF⊥OB?若存在,求出△AFB的面积.
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)由抛物线的定义,得4=3+
,即可得到抛物线方程和T的坐标;
(2)假设存在过M的直线l交抛物线于A、B(B在A的右侧)两点,使得直线AF⊥OB.
设直线AB:y=k(x+1),设A(x1,y1),B(x2,y2),联立抛物线方程,消去y,注意判别式大于0,运用韦达定理,由AF⊥OB得到
•
=-1.化简整理即可得到k,从而求出x1,x2,求得AF,BF,AB,求得△ABF的面积.
| p |
| 2 |
(2)假设存在过M的直线l交抛物线于A、B(B在A的右侧)两点,使得直线AF⊥OB.
设直线AB:y=k(x+1),设A(x1,y1),B(x2,y2),联立抛物线方程,消去y,注意判别式大于0,运用韦达定理,由AF⊥OB得到
| y1 |
| x1-1 |
| y2 |
| x2 |
解答:
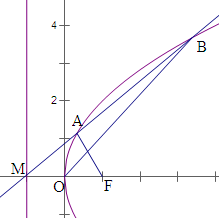 解:(1)由于抛物线y2=2px(p>0)上的点T(3,t)
解:(1)由于抛物线y2=2px(p>0)上的点T(3,t)
到焦点F的距离为4,由抛物线的定义,得4=3+
,p=2,
即有y2=4x,T(3,±2
),
则
=±
;
(2)假设存在过M的直线l交抛物线于A、B(B在A的右侧)两点,使得直线AF⊥OB.
M(-1.0),F(1,0),设直线AB:y=k(x+1),
设A(x1,y1),B(x2,y2),联立抛物线方程,消去y,
得k2x2+(2k2-4)x+k2=0,△=(2k2-4)2-4k4>0,即k2<1.
则x1+x2=
-2,x1x2=1.由AF⊥OB得到
•
=-1.
y1y2+x1x2-x2=0,即k2(x1+1)(x2+1)+x1x2-x2=0,即k2(x1+x2+x1x2+1)+1-x2=0,
k2(2+
-2)+1-x2=0,则x2=5,x1=
,5+
=
-2,k2=
<1,则k=±
.
故存在这样的直线为y=±
(x+1).
AF=
+1=
,BF=5+1=6,AB2=BF2-AF2=36-
=
,
故S△ABF=
AF•AB=
×
×
=
.
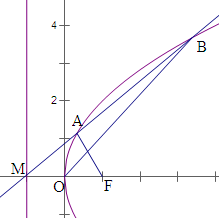 解:(1)由于抛物线y2=2px(p>0)上的点T(3,t)
解:(1)由于抛物线y2=2px(p>0)上的点T(3,t)到焦点F的距离为4,由抛物线的定义,得4=3+
| p |
| 2 |
即有y2=4x,T(3,±2
| 3 |
则
| t |
| p |
| 3 |
(2)假设存在过M的直线l交抛物线于A、B(B在A的右侧)两点,使得直线AF⊥OB.
M(-1.0),F(1,0),设直线AB:y=k(x+1),
设A(x1,y1),B(x2,y2),联立抛物线方程,消去y,
得k2x2+(2k2-4)x+k2=0,△=(2k2-4)2-4k4>0,即k2<1.
则x1+x2=
| 4 |
| k2 |
| y1 |
| x1-1 |
| y2 |
| x2 |
y1y2+x1x2-x2=0,即k2(x1+1)(x2+1)+x1x2-x2=0,即k2(x1+x2+x1x2+1)+1-x2=0,
k2(2+
| 4 |
| k2 |
| 1 |
| 5 |
| 1 |
| 5 |
| 4 |
| k2 |
| 5 |
| 9 |
| ||
| 3 |
故存在这样的直线为y=±
| ||
| 3 |
AF=
| 1 |
| 5 |
| 6 |
| 5 |
| 36 |
| 25 |
| 36×24 |
| 25 |
故S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 5 |
12
| ||
| 5 |
36
| ||
| 25 |
点评:本题考查抛物线的方程、定义和性质,考查联立直线方程和抛物线方程,消去未知数,运用韦达定理求解,注意检验,是一道中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
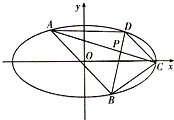 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆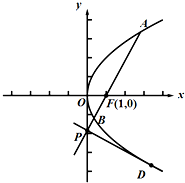 抛物线C:y2=2px(p>0),过抛物线C的焦点F(1,0)的直线l与抛物线交于A,B两点,交y轴于点P.
抛物线C:y2=2px(p>0),过抛物线C的焦点F(1,0)的直线l与抛物线交于A,B两点,交y轴于点P. 中国首届绿色运动会2011年10月18日至11月2日在安徽池州举行.绿运会期间,“上海城”举办了绿色产品展销会,并在展销会场设有购物满50元就获得一次有奖摸球活动.一个不透明的袋子中装有大小相同的8个球,其中标有1,2,3,4数字的球各2个,现从中任意抽取2个,用ξ表示抽取的这两个球上的数字之和.求:
中国首届绿色运动会2011年10月18日至11月2日在安徽池州举行.绿运会期间,“上海城”举办了绿色产品展销会,并在展销会场设有购物满50元就获得一次有奖摸球活动.一个不透明的袋子中装有大小相同的8个球,其中标有1,2,3,4数字的球各2个,现从中任意抽取2个,用ξ表示抽取的这两个球上的数字之和.求: