题目内容
在△ABC中,角A,B,C的对边为a,b,c.
(1)若2a=b+c,sin2A=sinBsinC,试判断△ABC的形状;
(2)试比较a2+b2+c2与2(ab+bc+ca)的大小.
(1)若2a=b+c,sin2A=sinBsinC,试判断△ABC的形状;
(2)试比较a2+b2+c2与2(ab+bc+ca)的大小.
考点:三角形的形状判断
专题:解三角形
分析:(1)首先根据正弦定理得出a2=bc,然后结合2a=b+c,得出b=c,a=b判断出三角形的形状;
(2)将要比较大小的两式作差后整理可得:a2+b2+c2-2(ab+bc+ac)=(a+b)(a-b-2c)+c2;①依题意知a+b>c,a-b-2c<0,利用不等式的性质即可得到答案.
(2)将要比较大小的两式作差后整理可得:a2+b2+c2-2(ab+bc+ac)=(a+b)(a-b-2c)+c2;①依题意知a+b>c,a-b-2c<0,利用不等式的性质即可得到答案.
解答:
解:(1)由正弦定理及sin2A=sinBsinC得a2=bc,又由2a=b+c得4a2=b2+2bc+c2,所以b2-2bc+c2=0,即(b-c)2=0,所以b=c.…(5分)
故a2=b2,即a=b,所以△ABC是等边三角形.…(7分)
(2)因为2(ab+bc+ca)-(a2+b2+c2)=(ab+ca-a2)+(ab+bc-b2)+(ca+bc-c2)=a(b+c-a)+b(a+c-b)+c(a+b-c),…(10分)
因为a,b,c为△ABC的三边长,故a>0,b>0,c>0,b+c-a>0,a+c-b>0,a+b-c>0,
所以a(b+c-a)+b(a+c-b)+c(a+b-c)>0…(13分)
故a2+b2+c2<2(ab+bc+ca).…(14分)
故a2=b2,即a=b,所以△ABC是等边三角形.…(7分)
(2)因为2(ab+bc+ca)-(a2+b2+c2)=(ab+ca-a2)+(ab+bc-b2)+(ca+bc-c2)=a(b+c-a)+b(a+c-b)+c(a+b-c),…(10分)
因为a,b,c为△ABC的三边长,故a>0,b>0,c>0,b+c-a>0,a+c-b>0,a+b-c>0,
所以a(b+c-a)+b(a+c-b)+c(a+b-c)>0…(13分)
故a2+b2+c2<2(ab+bc+ca).…(14分)
点评:本题考查正弦定理,着重考查作差法、二次函数的配方法、放缩法的综合应用,考查转化思想与推理运算能力,属于难题.

练习册系列答案
相关题目
已知偶函数y=f(x)在区间[0,+∞)为增函数,则f(-3)和f(π)大小关系是( )
| A、f(-3)>f(π) |
| B、f(-3)<f(π) |
| C、f(-3)=f(π) |
| D、不能确定 |
不等式组
所表示的平面区域的面积为( )
|
A、
| ||
| B、27 | ||
| C、30 | ||
D、
|
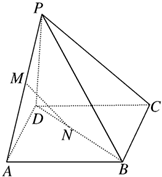 已知正方形ABCD的边长是13,平面ABCD外一点P到正方形各顶点的距离都为13,M、N分别是PA、BD上的点且PM:MA=BN:ND=5:8,如图.
已知正方形ABCD的边长是13,平面ABCD外一点P到正方形各顶点的距离都为13,M、N分别是PA、BD上的点且PM:MA=BN:ND=5:8,如图.