Question

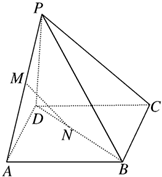已知正方形ABCD的边长是13，平面ABCD外一点P到正方形各顶点的距离都为13，M、N分别是PA、BD上的点且PM：MA=BN：ND=5：8，如图．
（1）求证：直线MN∥平面PBC；
（2）求线段MN的长．

Answer 1

考点：直线与平面平行的判定,点、线、面间的距离计算

专题：空间位置关系与距离

分析：（1）连结AN并延长和BC交于E点，由条件证明MN∥PE，再利用直线和平面平行的判定定理证明MN∥平面PBC．
（2）由于△PBC是边长为13的等边三角形，利用余弦定理求得PE的值，根据△AMN 与△APE的相似比为

8

13

，可得MN=

8

13

PE的值．

解答： （1）证明：连结AN并延长和BC交于E点，由PM：MA=BN：ND=5：8，可得EN：NA=BN：ND=MP：MA=5：8，
即

NE

NA

=

PM

MA

，∴MN∥PE，而MN?平面PBC，PE?面PBC，
∴MN∥平面PBC．
（2）解：由于△PBC是边长为13的等边三角形，
余弦定理求得PE²=PB²+BE²-2PB•EBcos60°=13²+(

13

2

)2-2×13×

13

2

×

1

2

=

8281

64

，
∴PE=

91

8

．
由于△AMN 与△APE的相似比为

8

13

，∴MN=

8

13

PE=7．

点评：本题主要考查直线和平面平行的判定定理的应用，余弦定理，体现了转化、数形结合的数学思想，属于基础题．