题目内容
117,182的最大公约数是 .
考点:用辗转相除计算最大公约数
专题:算法和程序框图
分析:本题考查的知识点是辗转相除法,根据辗转相除法的步骤,将117和182代入易得到答案.
解答:
解:∵182=1×117+65,
117=1×65+52,
65=1×52+13,
52=4×13,
故117,182的最大公约数是13,
故答案为:13
117=1×65+52,
65=1×52+13,
52=4×13,
故117,182的最大公约数是13,
故答案为:13
点评:对任意整数a,b,b>0,存在唯一的整数q,r,使a=bq+r,其中0≤r<b,这个事实称为带余除法定理,若c|a,c|b,则称c是a,b的公因数.若d是a,b的公因数,且d可被a,b的任意公因数整除则称d是a,b的最大公因数.当d≥0时,d是a,b公因数中最大者.若a,b的最大公因数等于1,则称a,b互素.累次利用带余除法可以求出a,b的最大公因数,这种方法常称为辗转相除法.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
函数f(x)=x2+2x,x∈[-2,1]的值域是( )
| A、[0,3] |
| B、[-2,3] |
| C、[-1,0] |
| D、[-1,3] |
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得几何体的体积是( )cm3.
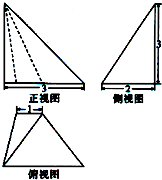

| A、4 | B、3 | C、6 | D、5 |
函数f(x)=ax2+bx+c,若f(1)<0,f(2)>0,则f(x)在(1,2)上零点的个数为( )
| A、至多有一个 |
| B、有一个或两个 |
| C、有且仅有一个 |
| D、一个也没有 |
已知函数f(x)=
,则该函数的定义域为( )
| 2x-1 |
A、{x|x>
| ||
B、{x|x≥
| ||
C、{x|x>-
| ||
D、{x|x≥-
|
已知向量
,
均为单位向量,若它们的夹角是60°,则|
-3
|等于( )
| a |
| b |
| a |
| b |
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|