题目内容
已知P是边长为2的正方形ABCD内的点,若△PAB,△PBC面积均不大于1,则
•
取值范围是( )
| AP |
| BP |
| A、(-1,2) | ||||
| B、[-1,1] | ||||
C、(0,
| ||||
D、[
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设点P(x,y),由已知条件可得x,y满足的可行域,利用数量积可得要求的问题,进而即可解决.
解答:
解:如右图所示: 设点P(x,y).
设点P(x,y).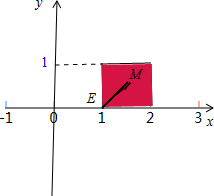
∵△PAB,△PBC面积均不大于1,
∴
×2y≤1,
×2×(2-x)≤1,0≤x≤2,0≤y≤2.
解得0≤y≤1,1≤x≤2.如左图所示的可行域:
由
•
=(x,y)•(x-2,y)=x(x-2)+y2=(x-1)2+y2-1.
∵d2=(x-1)2+y2表示的是可行域中的任意一点M与E(1,0)的距离的平方,
∴0≤d2≤(
)2,∴-1≤d2-1≤1,即-1≤
•
≤1.
故选B.
 设点P(x,y).
设点P(x,y).
∵△PAB,△PBC面积均不大于1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得0≤y≤1,1≤x≤2.如左图所示的可行域:
由
| AP |
| BP |
∵d2=(x-1)2+y2表示的是可行域中的任意一点M与E(1,0)的距离的平方,
∴0≤d2≤(
| 2 |
| AP |
| BP |
故选B.
点评:本题考查了向量的数量积;利用面积和向量的数量积正确得出x,y的取值范围及要解决的问题和充分结合图形是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
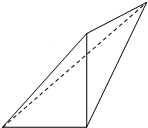 一个四面体如图,若该四面体的正视图(主视图)、侧视图(左视图)和俯视图都是直角边长为1的等腰直角三角形,则它的体积V=( )
一个四面体如图,若该四面体的正视图(主视图)、侧视图(左视图)和俯视图都是直角边长为1的等腰直角三角形,则它的体积V=( )A、
| ||
B、
| ||
C、
| ||
D、
|
若双曲线
-
=1(a>0,b>0)与直线y=
x无交点,则
的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| b |
| a |
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、[
|