题目内容
记集合A={(x,y)|
}、B={(x,y)|x2+y2≤1}构成的平面区域分别为M、N,现随机地向N中抛一粒豆子(大小忽略不计),则该豆子落入M中的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:先求出区域A的面积,然后利用圆的面积公式求区域B的面积,最后利用几何概型的概率公式解之即可.
解答:
 解:如图:集合A={(x,y)|
解:如图:集合A={(x,y)|
}、B={(x,y)|x2+y2≤1}构成的平面区域分别为M、N,分别为正方形与圆,随机地向N中抛一粒豆子(大小忽略不计),则该夹子落入M中的概率:就是
=
.
故选:A.
 解:如图:集合A={(x,y)|
解:如图:集合A={(x,y)|
|
| ||
| π12 |
| 1 |
| 4 |
故选:A.
点评:本题主要考查了几何概型的概率,以及利用圆的面积公式求区域面积,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
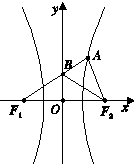 如图,双曲线C:
如图,双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、1+
| ||||
C、
| ||||
D、
|
已知P是边长为2的正方形ABCD内的点,若△PAB,△PBC面积均不大于1,则
•
取值范围是( )
| AP |
| BP |
| A、(-1,2) | ||||
| B、[-1,1] | ||||
C、(0,
| ||||
D、[
|
下列函数在其定义域内,既是奇函数又是单调递增函数的是( )
| A、y=sinx | ||
B、y=log
| ||
| C、y=x+8 | ||
| D、y=x3 |
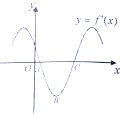 函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,A,C为图象与x轴的两个交点,B为图象的最低点,若在曲线
函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,A,C为图象与x轴的两个交点,B为图象的最低点,若在曲线 |
| ABC |
数列{an}中,已知a1=1,对任意的k∈N*,有a2k-1,a2k,a2k+1成等比数列,且公比为2k,则a101的值为( )
| A、2 502 |
| B、250×51 |
| C、2 512 |
| D、2101×102 |