题目内容

求下列椭圆的长轴长和短轴长、离心率、焦点坐标．
（1）x2+4y2=16；（2）9x2+y2=81．
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：化简两个椭圆为标准方程然后分求解长轴长和短轴长、离心率、焦点坐标．
解答： 解：（1）x2+4y2=16；化为：
x2
16
+
y2
4
=1，可得a=4，b=2，c=2
3
，故2a=8，2b=4，e=
3
2
，焦点坐标（±2
3
，0）．
（2）9x2+y2=81．化为：
y2
81
+
x2
9
=1，可得a=9，b=3，故2a=18，2b=6，c=6
2
，e=
2
2
3
，焦点坐标（0，±6
2
）．
点评：本题考查椭圆的简单性质的应用，基本知识的考查．
练习册系列答案
相关题目
在△ABC中，
AC
•
AB
I
AB
I
=1，
AB•
BC
I
AB
I
=-2，则AB边的长度为（　　）
A、1B、3C、5D、9
若偶函数f（x）满足f（x-1）=f（x+1），在x∈[0，1]时，f（x）=x2，则关于x的方程f（x）=（
1
10
）x在[0，4]上根的个数是
 
．
已知椭圆C的中心在坐标原点O，长轴在x轴上，离心率为
1
2
，且椭圆C上一点到两个焦点的距离之和为4．
（Ⅰ）椭圆C的标准方程．
（Ⅱ）已知P、Q是椭圆C上的两点，若OP⊥OQ，求证：
1
|OP|2
+
1
|OQ|2
为定值．
（Ⅲ）当
1
|OP|2
+
1
|OQ|2
为（Ⅱ）所求定值时，试探究OP⊥OQ是否成立？并说明理由．
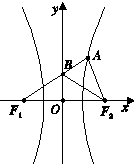如图，双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点F1（-c，0）、F2（c，0），A为双曲线C右支上一点，且|AF1|=2c，AF1与y轴交于点B，若F2B是∠AF2F1的角平分线，则双曲线C的离心率是（　　）
A、
3+
3
2
B、1+
3
C、
3+
5
3
D、
3+
5
2
设a＞b≥1，集合A={x|x∈Z，0＜x＜a}，B={x|x∈Z，-b＜x＜b}，记“从集合A中任取一个元素x，x∉B”为事件M，“从集合A中任取一个元素x，x∈B”为事件N．给定下列三个命题：
①当a=5，b=3时，P（M）=P（N）=
1
2
；
②若P（M）=1，则a=2，b=1；
③P（M）+P（N）=1恒成立．
其中，为真命题的是（　　）
A、①②B、①③C、②③D、①②③
已知P是边长为2的正方形ABCD内的点，若△PAB，△PBC面积均不大于1，则
AP
•
BP
取值范围是（　　）
A、（-1，2）
B、[-1，1]
C、（0，
1
2
]
D、[
1
2
，
3
2
）
下列函数在其定义域内，既是奇函数又是单调递增函数的是（　　）
A、y=sinx
B、y=log 
1
2
x
C、y=x+8
D、y=x3
在等差数列{an}中，已知a4=10，且a3，a6，a10成等比数列．
（1）求an；
（2）设bn=2 an（n∈N*），求数列{bn}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网